A uniform flexible chain on a smooth sphere
- As shown in the figure, the top of a uniform flexible chain market in RED color ,which is length pi * R/3, it is fixed on a smooth sphere with radius R, as shown in the figure.
Now, release the top of the chain.
When it was just released, what position on the chain had the greatest tension?
note: Gravity acceleration g = 9.8 m/s2
The answer should be in range from 0 to 90 degrees
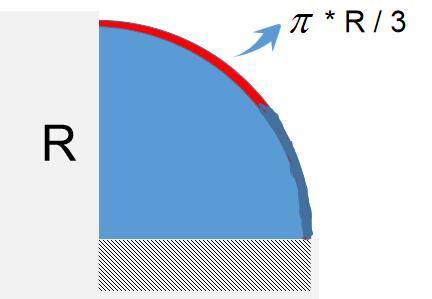
The answer is 28.52.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice problem. Please mention in the problem that the angular position is measured from the top
Thank you,60 degree or pi * R/3
Log in to reply
I was referring to the answer itself. Whether the answer is supposed to be 28.52 measured from the vertical downward, or whether it is (90 - 28.52), measured from the horizontal upward. Just so people don't waste tries assuming the wrong convention.
Log in to reply
exactly the answer is supposed to be 28.52 measured from the vertical downward
Measure the angle ϕ from the vertical direction. A segment of the chain between ϕ and ϕ + d ϕ has a mass of ρ d ϕ , where ρ is a constant. The tangential tension force pulling this segment backwards is F , the tension pulling forward is F + d F and the tangential component of the gravitational force is ρ g sin ϕ d ϕ . Newton's law for this segment is
( ρ g sin ϕ ) d ϕ − F + F + d F = ( a ρ ) d ϕ
where a is the magnitude of the acceleration that is independent of the angle ϕ . This leads to
ρ g 1 d ϕ d F = g a − sin ϕ
We solve this differential equation with the boundary condition that the tension is zero at ϕ = 0 and at ϕ = π / 3 . The solution is
ρ g F = g a ϕ + c o s ϕ − 1
where g a = 2 π 3 , otherwise the boundary condition is not satisfied. The force is maximum when d ϕ d F = 0 , or ρ g 1 d ρ d F = g a − sin ϕ = 0 . This yields
ϕ = sin − 1 2 π 3 = 2 8 . 5 2 o
Just released, the whole chain slides at the same acceleration rate against the sphere. Consider a slip of a small displacement of the whole chain
The kinetic energy corresponding to this velocity should be converted from part of the gravitational potential energy during the chain's descent. When calculating the change of gravitational potential energy, it is equivalent.
It is considered that the length of the top of the chain is *dl * is tiny length of chain A small section is transferred directly to the end. Note that the linear density of chains is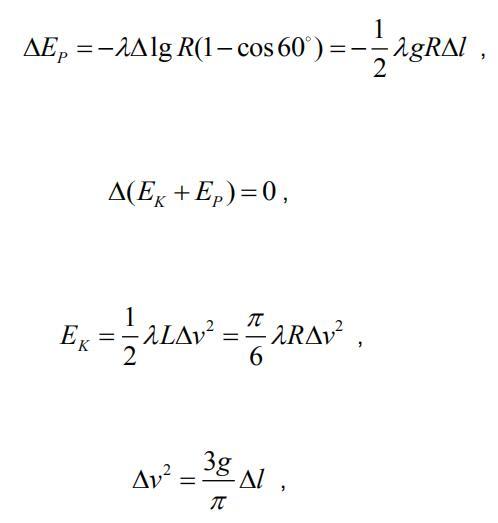
The quality of this section is Gravitational potential

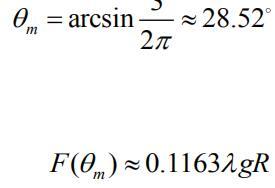
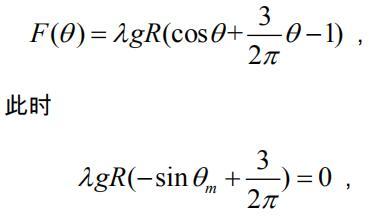
Can change to
Every point on the chain moves in a circle. Since the velocity is zero at the time of release, the centripetal acceleration is zero, and only the size of the phase is different. Equal tangential acceleration When discussing the velocity change in a small process, it can always be regarded as uniformly accelerated linear motion.