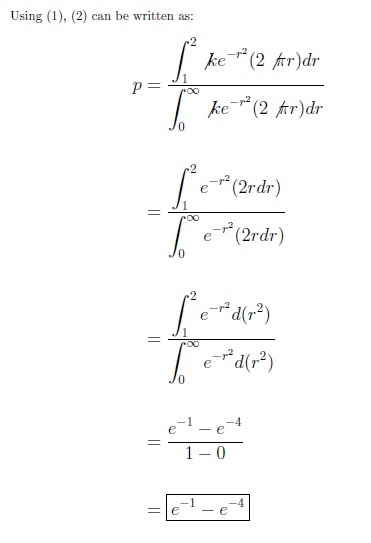A Unique Game

You are playing a game of darts on an infinite board which can be thought of as the XY Plane where every position can be denoted by its x and y co-ordinates.

Your score (which can be rational or irrational) depends on the position (x,y) where the dart lands and is given by the function:

$S(x, y) = e^{-\big(x^2 + y^2 - 3\sqrt{x^2 + y^2} + 2\big)}$

However, you can't reach every point with equal probability and the relative probability that you hit a point (x, y) is given by:

$P(x, y) \propto e^{-\big(x^2+y^2\big)}$

You throw one dart, what is the probability that your score is more than 1?

Enter your answer to five decimal places.