A Useful Result

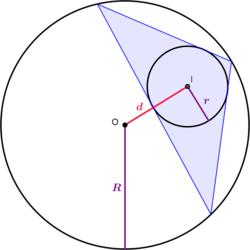
This is known as Euler's Triangle Formula. The distance $d$ between the incenter and the circumcenter is $d=\sqrt{R(R-2r)}$ , where $R$ is the circumradius and $r$ is the inradius. To find $d$ , we must first find $R$ and $r$ .

Finding $R$ is easy. The triangle is a 6-8-10 pythagorean triple, which makes it a right triangle. Right triangles inscribed in a circle always have their hypotenuse on the diameter, therefore our circumradius must be half of the hypotenuse, making $R=\frac{10}{2}=5$ .

Finding $r$ is a bit harder, but we can actually calculate it using the value of our circumradius. The inradius and the circumradius are related by the following equation:

$r=\frac{abc}{2R(a+b+c)}\text{, where } a \text{, } b \text{ and } c \text{ are the sides of the triangle.}$

Plugging in $R=5$ , $a=6$ , $b=8$ and $c=10$ gives us $r=\frac{(6)(8)(10)}{2(5)(6+8+10)}=2$ .

Finally, all that's left to do is plug in $R=5$ and $r=2$ into our equation for $d$ and we're done!

$d=\sqrt{5(5-2(2))}=\sqrt{5}=\boxed{2.236...}$

IMHO, since we're dealing with a right triangle, an easier way to do this would be to consider the following triangle -- O:(0,0), A:(6,0) & B:(0,8). The in-centre is clearly at (2,2) and the circum-centre at (3,4). So the required distance = √[(3-2)²+(4-2)²] =√5~2.2361