A very big number

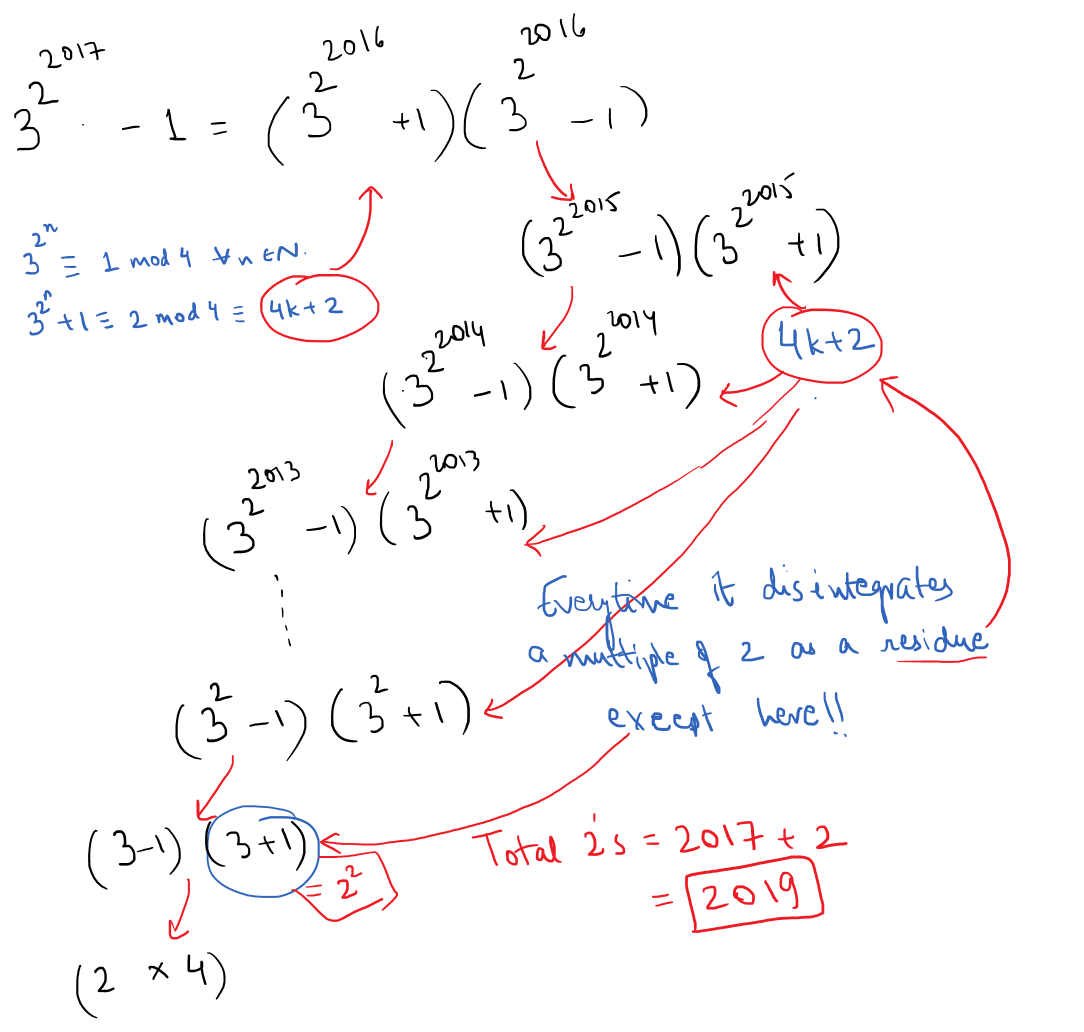
We will prove the general case $3^{2^x} - 1$ . We use the Difference of Perfect Squares identity to factorise this expression:

$\begin{aligned} 3^{2^x} - 1 &= (3^{2^{x-1}} + 1) (3^{2^{x-1}} - 1)\\ &= (3^{2^{x-1}} + 1)(3^{2^{x-2}}+1)(3^{2^{x-2}}-1)\\ &= (3^{2^{x-1}} + 1)(3^{2^{x-2}}+1) \ldots (3^2 + 1) (3+1)(3-1) \end{aligned}$

Notice that each bracket to the left of $(3+1)$ are equivalent to $2 \pmod{4}$ , so 2 divides each of those brackets, but 4 does not. There are $x-1$ terms, so at least $2^{x-1}$ divides $3^{2^x} - 1$ . Also, $(3+1)(3-1)=2^{3}$ , so we must have $2^{x+2} \mid 3^{2^x}-1$ . Thus, the maximum value of $n$ is $x+2$ .

Substituting $x=2017$ , we get $n=\boxed{2019}$ .

---

Quick, slick solution:

We use the Lifting the Exponent Lemma.

$v_2 (3^{2^{x}} - 1) = v_2 (3 + 1) + v_2 (2^x) = x+2$

Thus, $n=2019$ .

3^x=(4-1)^x . So, expanding (4-1)^x =(4^x) - (4^x-1)x+.......+(-1)^x In this case as x is even so (-1)^x is 1 So, there fore.
(4-1)^x - 1 will be 4^x - x(4^x-1)+....-4x So, 4x is common in each term so it is divisible by 4x As x=2^2017, So 4x =2^2019 So finally we get n= 2019

direct use of lifting the exponent theorem