A very hard problem indeed
A quadrilateral has the following vertices: . We want to circumscribe the quadrilateral with an ellipse passing through its four vertices. There is an infinite number of ellipses satisfying this property. Find the one with the minimum area , and enter as your answer.
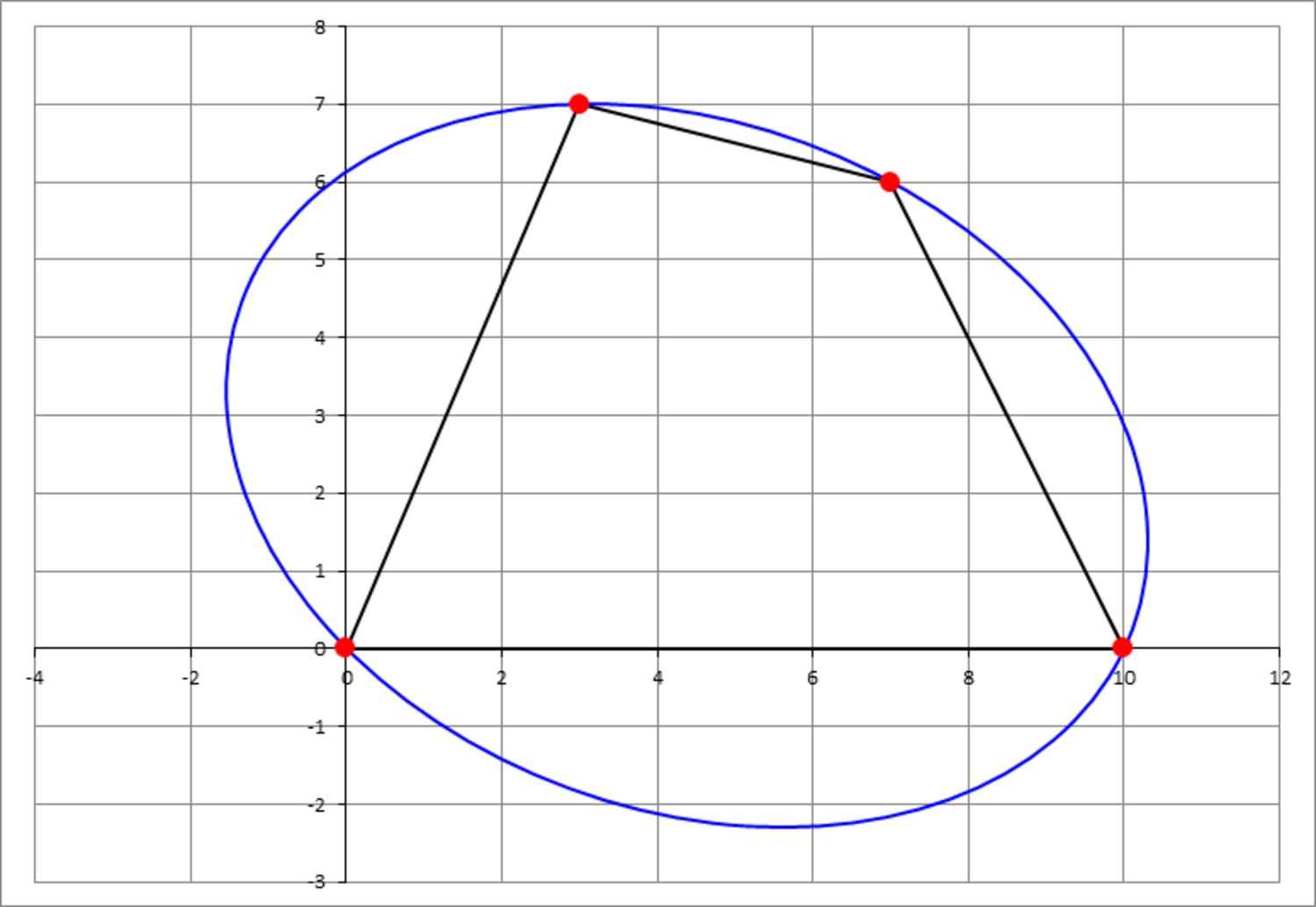
The answer is 8466.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
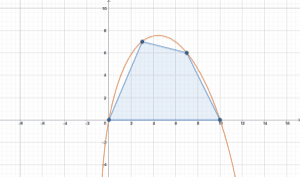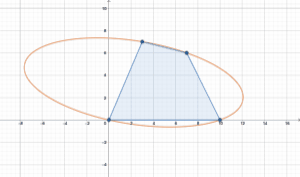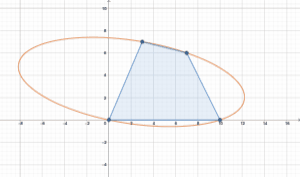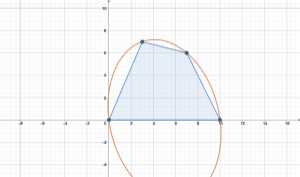
The general equation for an ellipse is A x 2 + B x y + C y 2 + D x + E y + F = 0 where B 2 − 4 A C < 0 .
Since this ellipse passes through ( 0 , 0 ) , we must have F = 0 . Without loss of generality, we can take A = 1 , to leave the equation as x 2 + B x y + C y 2 + D x + E y = 0
The point ( 1 0 , 0 ) tells us that 1 0 0 + 1 0 D = 0 ie that D = − 1 0 .
Updating our equation, x 2 + B x y + C y 2 − 1 0 x + E y = 0
The other two points tell us that 4 9 + 4 2 B + 3 6 C − 7 0 + 6 E 9 + 2 1 B + 4 9 C − 3 0 + 7 E = 0 = 0
We have two equations in three unknowns; although this means we can't solve the system completely, we can parameterise two of the unknowns in terms of the third. Choosing (arbitrarily) B as the parameter, we get C = 4 B − 2 1 , E = 2 1 3 − 3 1 B
So (almost) the whole family of conics passing through the given points are parameterised as x 2 + B x y + ( 4 B − 2 1 ) y 2 − 1 0 x + ( 2 1 3 − 3 1 B ) y = 0
This form in fact includes conics that are not ellipses, but we'll deal with those later. It also excludes conics where (in the original general form) A = 0 ; however, these cannot be ellipses, so - for this problem - we're not interested in them.
Now we turn to the area enclosed. We can work out expressions for the semi-major and semi-minor axes of the ellipse ( a and b ) in terms of the coefficients A to F ; or we can look them up, eg here .
The area of the ellipse is π a b . This works out as T = π a b = ( 4 A C − B 2 ) 2 3 2 π ( A E 2 + C D 2 − B D E + ( B 2 − 4 A C ) F )
This is where we can look at what happens when the conic is not an ellipse. Note that for the denominator to be real and non-zero, we need 4 A C > B 2 ; but this is exactly the condition for the conic to be an ellipse. This makes intuitive sense; if a conic encloses an area, it must be an ellipse.
Putting everything together and tidying up, we have T = 2 ( − B 2 + 1 6 B − 2 ) 2 3 3 1 π ( 8 4 B 2 + 8 B − 1 )
Setting the derivative equal to zero gives the equation 8 4 B 3 + 6 8 8 B 2 − 4 0 3 B + 8 = 0
Solving this numerically, the minimum area is found when B ≈ 0 . 5 2 9 5 6 , giving area T ≈ 8 4 . 6 6 4 and answer 8 4 6 6 .