A Walk on the Coordinate Plane Pt.2

Imagine that the point $(x,y)$ is in the region. That means that there exists a path from $(-1,0)$ to $(1,0)$ that crosses that point, as well as a path from $(0,-1)$ to $(0,1)$ that crosses it. Let's now connect the point $(x,y)$ with all those points via straight lines (see the picture). This creates the shortest possible path that passes through $(x,y)$ and passes through a pair of points. The first path has length $d((-1,0),(x,y)) + d((x,y),(1,0))$ and the other one $d((0,-1),(x,y)) + d((x,y),(0,1))$ . If these distances are equal to 3, then these are the required paths. If any of these distances is smaller than 3, we can imagine ourselves modifying the straight path, perhaps curving it up slightly to continuously increase its length until we reach a length of 3. This would be a proper path. Finally, if any of these distances is longer than 3 then it is impossible to find a path linking the two points because if the shortest distance is too big, any other distance will be too big.

So a point $(x,y)$ is in our region if and only if $d((-1,0),(x,y)) + d((x,y),(1,0)) \leq 3 \\ d((0,-1),(x,y)) + d((x,y),(0,1) \leq 3$

We know from the definition of the ellipse that these conditions both define ellipses and so our region will be the intersection of the ellipses defined by the inequalities. In fact, without much prior knowledge, we can algebraically discover the equation of the ellipses by the following computation. Let $u = x^2 + y^2 + 1, v = 2x$

$\sqrt{(x+1)^2 + y^2} + \sqrt{(x-1)^2 + y^2} \leq 3 \\ \sqrt{u + v} + \sqrt{u - v} \leq 3 \\ 2u + 2\sqrt{u^2 - v^2} \leq 9 \\ u + \sqrt{u^2 - v^2} \leq 4.5 \\ \sqrt{u^2 - v^2} \leq 4.5 - u \\ u^2 - v^2 \leq 4.5^2 - 9u + u^2 \\ -v^2 \leq 20.5 - 9u \\ 9u - v^2 \leq 20.5 \\ 9x^2 + 9y^2 + 9 - 4x^2 \leq 20.5 \iff 5x^2 + 9y^2 \leq 11.5$

Similarly, the other inequality determines the ellipse $9x^2 + 5y^2 \leq 11.5$ . The region is then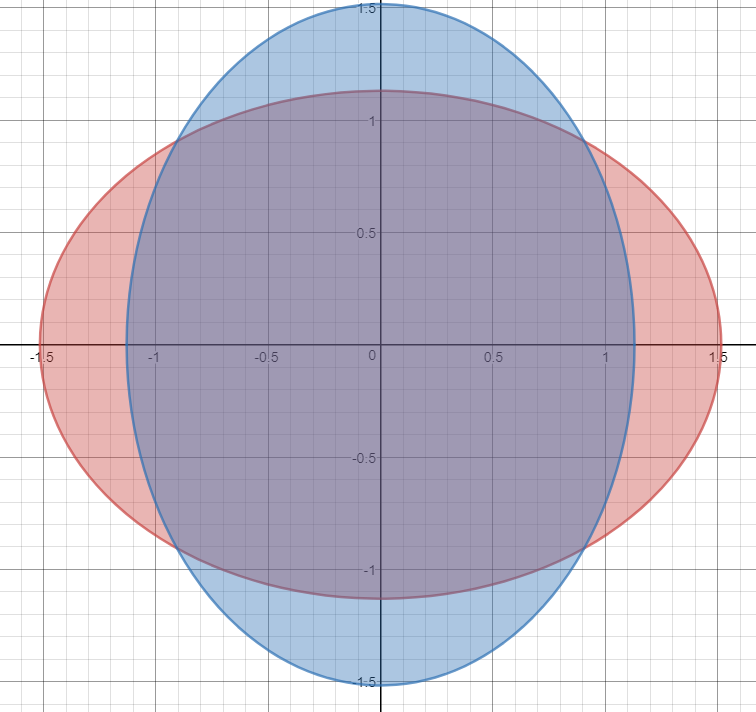

Now computing the area is nothing more than a standard calculus exercise which I will skip. One could either choose to parametrize the intersection of the two regions or to do a normal integral to find the area of one of the 4 bits that stick out and then subtract that twice from the area of the ellipse (which can be computed with the known formula).

The final solution is a bit ugly but obtainable with known constants:

$\frac{3 \sqrt{5}(\frac{\pi}{2} - \arcsin \left( \frac{2}{7} \right))}{2}$