A weird arrangement .
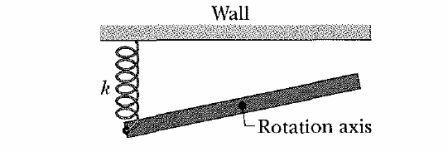 In the overhead view of the figure, a long uniform rod of mass
0
.
6
0
0
k
g
is free
to rotate in a horizontal plane about a vertical axis through its center.
A spring with force constant
κ
=
1
8
5
0
N
/
m
is connected horizontally
between one end of the rod and a fixed wall. When the rod is in equilibrium,
it is parallel to the wall. What is the period of the small oscillations
that result when the rod is rotated slightly and released
In the overhead view of the figure, a long uniform rod of mass
0
.
6
0
0
k
g
is free
to rotate in a horizontal plane about a vertical axis through its center.
A spring with force constant
κ
=
1
8
5
0
N
/
m
is connected horizontally
between one end of the rod and a fixed wall. When the rod is in equilibrium,
it is parallel to the wall. What is the period of the small oscillations
that result when the rod is rotated slightly and released
Liked it? Try more here
The answer is 0.0653.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
The reason the torque would be approximately 4 − 1 L 2 k θ is because the spring is compressed by an amound 2 L sin ( θ ) therefore the force is − k 2 L sin ( θ ) which is acting at a distance 2 L therefore the torque is − k ( 2 L ) 2 sin ( θ ) but since θ is small, we can make the approximation: sin ( θ ) ≈ θ
Therefore τ ≈ ( 4 − 1 ) k L 2 θ
Suppose r is half the length of the rod. Then if F is the force that is acting upon it due to the spring
F ⋅ r = I θ ¨
Where I is the moment of inertia of the rod and θ is the angle the rod makes with the wall. For small θ one is allowed to write
θ ≈ sin θ = r Δ x ∴ Δ x = r θ
Which means that F = − k Δ x ≈ − k r θ . Therefore, according to the first equation
− k r 2 θ ≈ I θ ¨ = 3 m r 2 θ ¨
Where we have used I = m r 2 / 3 . Therefore
θ ¨ + m 3 k θ ≈ 0 ⇒ T ≈ 2 π 3 k m ≈ 0 . 0 6 5 3 s
Let E be the energy of the system which remains conserved. When one end of the rod has undergone a small displacement ′ x ′ [Where x = 2 l θ ] .
E = 2 I ω 2 + 2 k x 2
Differentiating both sides
2 I d t d ω 2 + 2 k d t d x 2 = 0
2 I 2 ω d t d ω + 2 k 2 x d t d x = 0
I l 2 v d t 2 d 2 θ + k x v = 0
d t 2 d 2 θ + 4 I k l 2 θ = 0
Comparing with equation of differentiability
ω = 4 I k l 2 = m 3 k
T = 2 π 3 k m ≈ 0 . 0 6 5 3 s
Time period will be: T = 2 π 3 k m
I will call the length of the rod L and the mass M
Since the angle is small, the torque would be approximately 4 − 1 L 2 k θ and the rotational inertia is 1 2 M L 2 therefore the angular acceleration is approximately M − 3 k θ which gives you the following differential equation:
d t 2 d 2 θ = M − 3 k θ
This is the simple harmoic motion differential equation and it's solution is:
θ = ϕ s i n ( M 3 k t ) Where ϕ is the maximum angular displacement
The period of the sine function is 2pi, therefore the period of the oscillation is the T that satisfies M 3 k T = 2 π
So solving for the period, T, you get:
T = 2 π 3 k M