A white whale of a physics problem

Classical Mechanics Level 5

There's a lot of forces involved in sailing - there's the thrust force provided by the wind, gravitational forces on the boat, drag forces from the water and air, etc. Balancing all these forces sometimes requires sailors to take precarious positions (as Hollywood has used to great effect.)

Consider a sailboat floating in the water at some instant in time. In x,y,z coordinates the bottom of the mast is located at the origin and the top of the mast is at (0,0,8) m, while the boat itself is oriented along the y-axis. The sail is approximately a triangle, and the three end points of the sail are near the bottom of the mast at (0,0,1), at the top of the mast at (0,0,8), and at (2.858,2.858,1). A gust of wind comes along, blowing towards the positive x-direction at a speed of 20 km/hr. The collision of the air molecules with the sail can be taken to be perfectly elastic.

What is the magnitude of the force in Newtons on the boat exerted by the gust of wind?

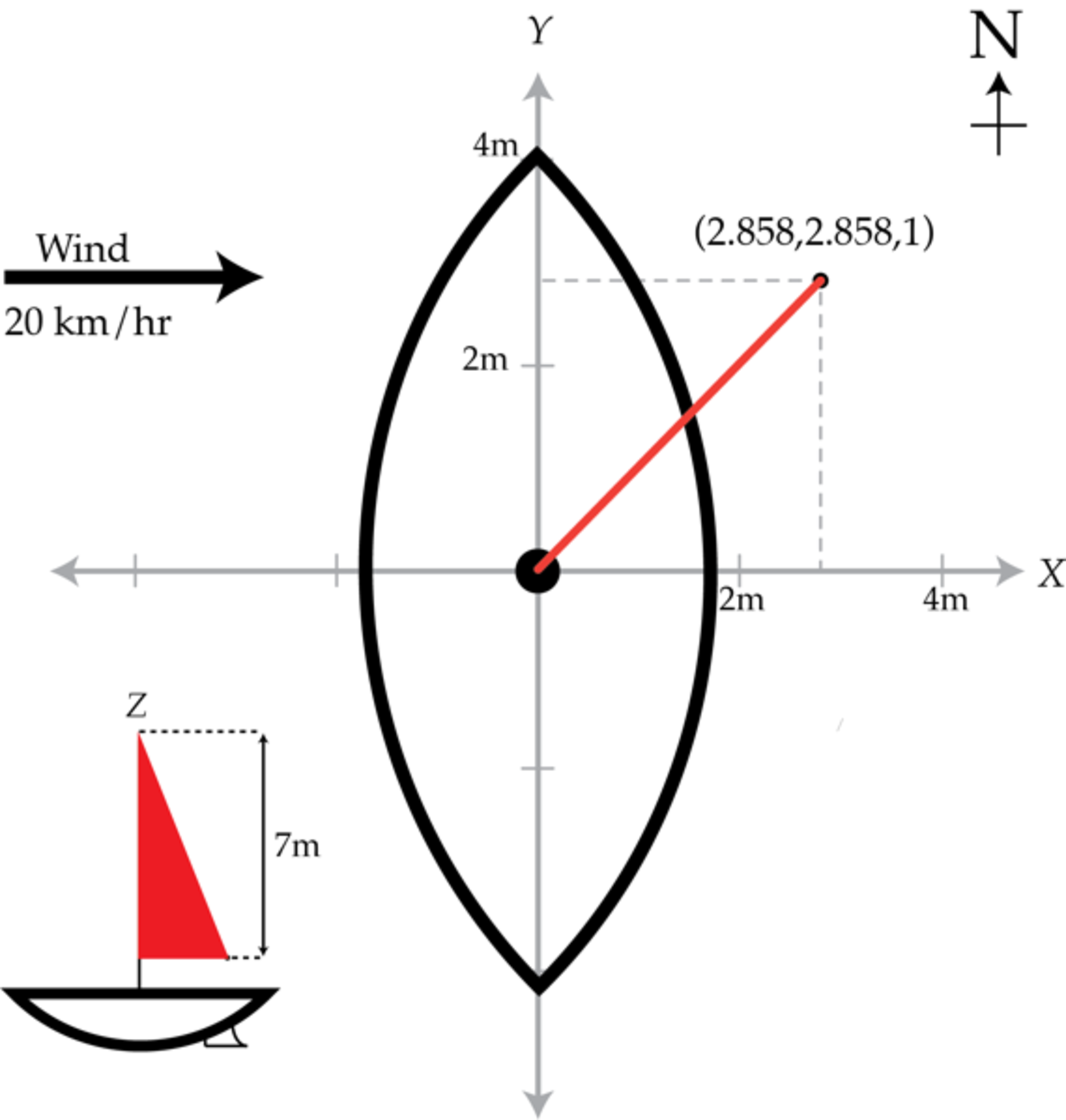
Details and assumptions

The density of air is $1.2~kg/m^3$ .
You may assume the boat is heavy enough that the gust does not make the boat move appreciably.

The answer is 523.94.

4 solutions

David Garcia
May 20, 2014

Convert units 20km/h to 5.56 m/s.

Determine area of the sail: 14.15 m^2.

(Area)(velocity)(cos(45)) represents the flux of air through the sail = $55.6 m^3/s$ .

(Flux of air)(density of air) represents kg/s of air impacting the sail= 66.7 kg/s.

Assume an arbitrary $\delta T$ over which the air impacts the sail.

Assume that $(kg/s~of~air)(\delta T)$ is equal to the mass of air (M) deflected by the force of the sail on the air.

Because the collision is elastic, the final speed of the air off the sail will equal the initial speed given in the problem, with a new direction. The initial momentum will be 5.56(M) in the x-direction and the final momentum will be 5.56(M) in the y-direction.

The change in momentum is equal to $-371\delta T$ in the x-direction $+371\delta T$ in the y-direction.

Change in momentum is equal to an applied force vector times the time of application, so I divided my momentum expression by $\delta T$ resulting in a force vector with components (-371,371).

The magnitude of this force vector is equal to $371\sqrt{2}=524$ N.

Armaan Bhullar
May 20, 2014

first we see that mass of air striking per second = X= projcted area×speed×density=.5 × 2.858 × 7 ×1.2 ×20000 ÷ 3600=66.68 now,magnitude of change in momentum =√(2)×magnitude of initial momentum. so ,by newtons third law,force on sail =X × speed× √(2) =523.9 newton

Kyriakos Grammatikos
May 20, 2014

For an infinitesimal air element of mass $dm$ ,the corresponding impulse transferred to the sail is calculated to be:

$dp=dm\cdot{2v\cos{\frac{\pi}{4}}}\iff$ $F=\frac{dp}{dt}=\frac{dm}{dt}\cdot {2v\cos{\frac{\pi}{4}}}$

Now ,using the conservation of mass and the given velocity field we can deduce that the rate of air mass coming through the projection of the sail on the YZ is the same as the rate of air mass hitting the sail. It follows that:

$\frac{dm}{dt}=\rho\frac{dV}{dt}=\rho{S}\frac{dx}{dt}=ρSv$

where S is the surface area of the projection of the sail. Finally, the total force exerted on the boat is:

$F=2\rho{S}v^2\cos{\frac{\pi}{4}}= 523.94 (N)$

Dingding Dong
May 20, 2014

The area of the flag is 2.858 * \sqrt{2} * (8-1) * 0.5m^2 The velocity of the wind is \frac {50}{9} meters per second, so the volume of the wind blowing to the flag in a secend is \frac {50}{9} * 2.858 * \sqrt{2} * 7 * 0.5= 78.6 m^3. The density of air is 1.2kg/m^3, so the mass of that wind is 78.6 * 1.2 = 94.3kg. We have the theorem of momentum which is mv = Ft, and m = 94.3kg, v = \frac {50}{9}m/s, and t = 1s. So F = 94.3 * \frac {50}{9} =523N

A white whale of a physics problem

The answer is 523.94.

4 solutions

0 pending reports