A Wrapped set of Four Tangent Spheres

The volume can be broken up into parts: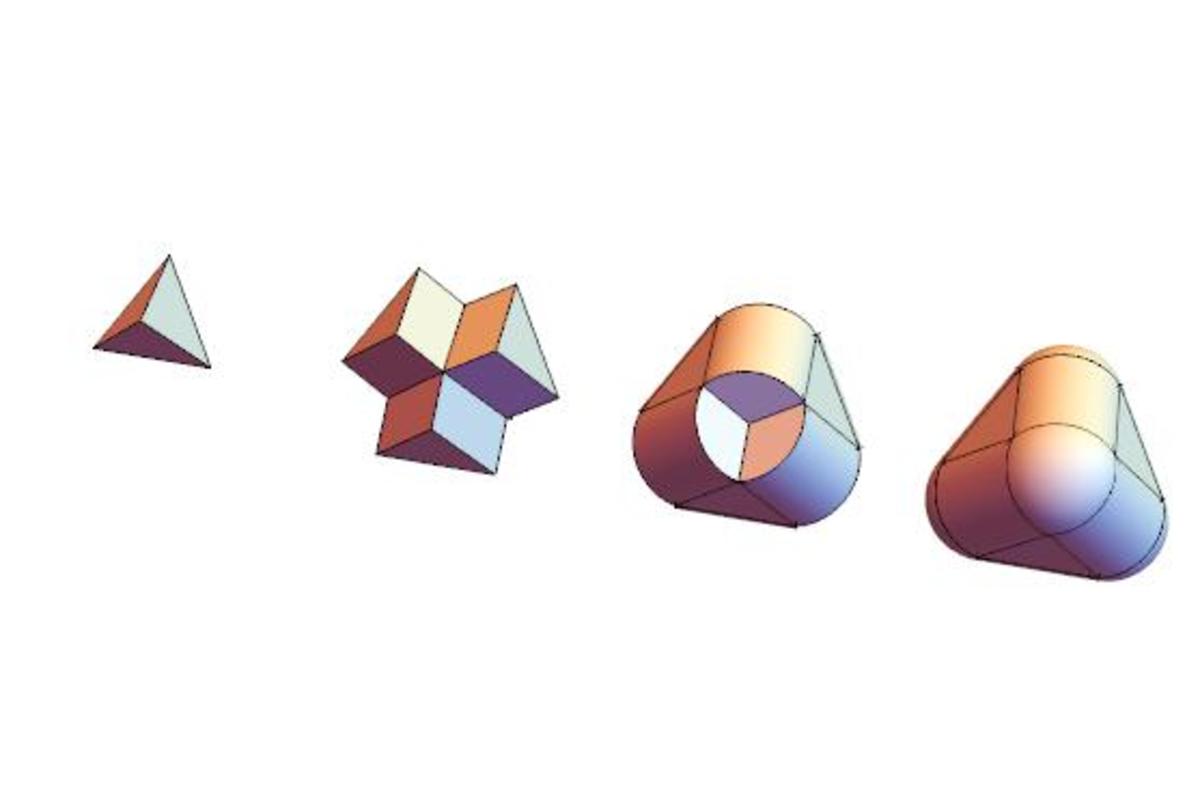

• the tetrahedron formed by the centres of the four spheres, which has volume $\tfrac{\sqrt{8}}{3}R^3$ ,
• four prisms, each of height $R$ and cross-section an equilateral triangle of side $2R$ (each of volume $\sqrt{3}R^3$ ),
• six prisms. each of height $2R$ , with cross-section a sector of a circle of radius $R$ with angle $\pi-\alpha$ , where $\alpha = \cos^{-1}\tfrac13$ is the dihedral angle of the tetrahedron (each has volume $(\pi - \alpha)R^3$ ),
• four vertex "caps", which fit together to form a single sphere of radius $R$ .

The four triangular prisms fit onto the faces of the inner tetrahedron, the other six prisms then fit along the edges of that tetrahedron, and the vertex caps fit into the gaps at the vertices of that tetrahedron.

The total volume enclosed by the sheet is $\tfrac43\pi R^2 + 4\sqrt{3}R^3 + 6(\pi - \alpha)R^3 + \tfrac{\sqrt{8}}{3}R^3 \;,$ and so the answer is $a \; = \; \tfrac43\pi + 4\sqrt{3} + 6(\pi - \alpha) + \tfrac{\sqrt{8}}{3} \; = \; \boxed{23.5236} \;.$