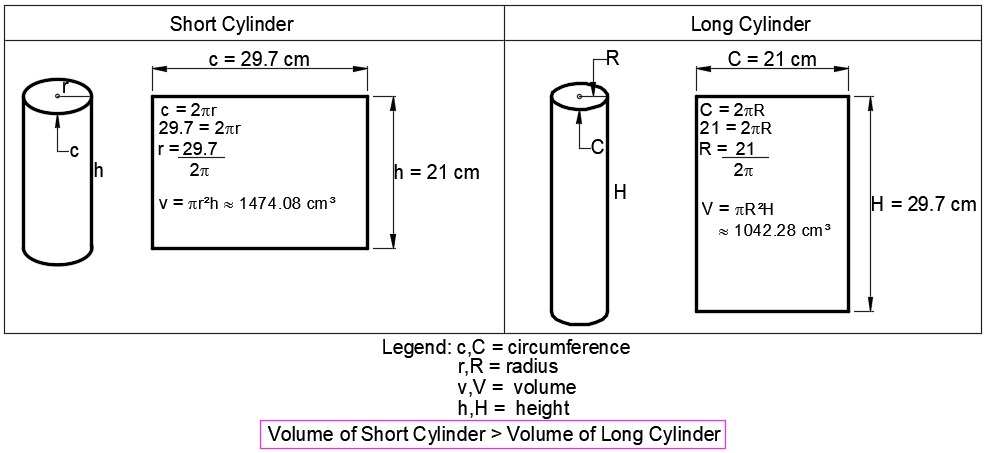
A4 Cylinder

As the circumference of a circle formula is $C = 2\pi r ,$ we also know $r = \frac{C}{2\pi} .$

The volume of a cylinder formula is $V = \pi r^2h .$ Substituting the previous formula, we also have $V = \pi \left(\frac{C}{2\pi}\right)^2h = \frac{1}{4\pi}C^2h .$

In the short cylinder the length $L$ of the paper is the circumference and the width $W$ of the paper is the height. The tall cylinder has the two variables reversed. That is, we are comparing:

$\frac{1}{4\pi}L^2W \quad \text{(short)} \quad \mathbf{VS.} \quad \frac{1}{4\pi}W^2L \quad \text{(tall)}$

In trying to figure out which is larger, we can remove the constants as they are identical in both; we can also divide both sides of our mystery inequality by $L$ and $W$ (as they are both positive), which after cancellation leaves us comparing $L$ of the short cylinder to $W$ of the tall one.

As the length (29.7 cm) is larger than the width (21.0 cm), the short cylinder has the larger volume.

Let the paper have length $a$ and $b$ while $a<b$ . When making a tall, slimmer cylinder, the radius would be $\frac{a}{2\pi}$ , tall be $b$ , so the volume would be $V_1=\frac1{4\pi}a^2b$ Same thing, the volume of another would be $V_2=\frac1{4\pi}ab^2$ By taking the ratio of two, we get $\begin{aligned}\frac{V_1}{V_2}&=\frac ab\\&<1\\\therefore V_1&<V_2\end{aligned}$ The fatter, the bigger.

For the two cylinder options we know the hight and the circumference of each.

 Long cylinder:  Height = 29.8                      Short cylinder:  Height = 21
                 Circumference = 21                                  Circumference = 29.8

To get the volume of a cylinder we use the

 Volume = Height * Area 

 We have the Height. The area is the circle formed at the top or bottom of the cylinder.

 The equation for area of a circle is 
      Circle area = πR^2
 But we dont have R (radius)

 However the equation for circumference of a circle is 
      Circumference = 2πR

Out of this we can calculate the Radius of each cylincer

 Long     Circumference = 21 = 2πR                  Short     Circumference = 29.8 = 2πR
                          21/2π = R                                           29.8/2π = R
                          R = 3.3422...                                       R = 4.7428...

Now we can use the Circle area equation

 Long     Circle area = πR^2                        Short     Circle area = πR^2
                      = π * (3.3422...)^2                                 = π * (4.7428...)^2
                      = 35.09366...                                       = 70.6679...

Now we just need to multiply with the height

 Long     Volume = Height * Area                    Short     Volume = Height * Area
                 = 29.8 * 35.09366...                                = 21 * 70.6679...
                 = 1045.79                                           = 1484.02

So now we can see that the Shorter cylinder has a bigger volume

Of all solids with a given surface area, the sphere has the greatest volume. A squat cylinder is more like a sphere than a skinny cylinder. Therefore I chose the short one.

If you want more detail, sure: the volume is proportional to the height and quadratically proportional to the circumference of the cylinder. Therefore the volume is optimized by using the longer side for the circumference. Even more precisely, the volume ratio is the ratio of the sides, $\sqrt 2:1$ .

Formulas: $circumference = 2* \pi * radius;~volume = \pi * radius^2 * height$

$(bigger\ number)^2\times\ (smaller\ number)$ $>$ $(the\ same\ smaller\ number)^2\times\ (the\ same\ bigger\ number)$

The smaller cylinder has the larger radius. Cancelling all other constants out, the final equation waters down to the above form. Therefore, the smaller cylinder has the larger volume.

The shorter cylinder is closer to a sphere than the taller one.

More simply, both cyclinders use 100% of the paper to form the hypothetical container. The short, fat one uses more empty space (i.e. the bottom) to form the hypothetical container, and therefore must be capable of holding more volume.

The volume of a cylinder is proportional to its height, but to the square of its radius. Therefore the radius should be maximised as a higher priority than its height. Therefore the length should be used as the radius.

The ratio volume/surface is equal to (pi D^2 L/4)/(pi D Lf)= D/4 Lets call 'a' this ratio, so a= D/4

I think we can say that if surface doesn't change, volume increases linearly with D

Volume of cylinder is $V \propto r^{2}\cdot H$ , so it's obvious that replacing $r$ for a bigger value will yield more volume.

When calculating the volume of a cylinder; the Height is powered only 1 but the RADIUS IS SQUARED. So, without making many calculation you can say that the fat one has bigger volume since its radius is bigger.

We know that the volume of a cylinder is given by: V= π (r∧2) h, being r the radius and h the height, so in this case where the two forms are created with the same sheet, all depends on the radius, the longer the radius, the bigger the volume of the cylinder, hence the reason why the short cylinder has a bigger volume

I didn’t use any calculations on this one, I simply imagined that each cylinder end was material and not just abstract.

By observing the sheet of paper as it is, the surface area is always the same regardless of its orientation, however, if you imagine the ends of the cylinders as material, and therefore part of the sheet of paper, it’s quite clear that the ends on the short cylinder have more surface area than those on the long one, no maths needed as you can see it! By my understanding, volume is positively proportional to surface area (shoot me if I’m wrong, maths isn’t my forté).

Add the surface area of the ends to the surface area of the sheet of paper in its original state and there you have your answer; the short cylinder (with closed ends) has more surface area therefore has more volume.

$\frac{((\frac{H}{2})^2\times W)}{((\frac{W}{2})^2\times H} = \frac{H}{W}$

Because H is bigger then W, the shorter cylinder has more volume. The fact that this ratio is $\sqrt{2}$ is a coincidence.

The outer surface area of both cylinders 1 and 2 are the same (same sheet of paper). So $2*pi*r_1*h_1 = 2*pi*r_2*h_2$ -> $r_1*h_1 = r_2*h_2 ..........eq_1$

The ratio of the volumes is $pi*(r_2^2)*h_2/pi*(r_1^2)*h_1$ or $pi*r_2*r_2*h_2/pi*r_1*r_1*h_1$ .

Since $r_1*h_1 = r_2*h_2$ , this ratio is directly proportional to $r_2/r_1$ (after canceling out the common factors in the numerator and denominator, namely $pi$ and $r_1*h_1$ , which is the same as $r_2*h_2$ from $eq_1$ )

Thus, if $r_2>r_1$ , then the volume of cylinder 2 > volume of cylinder 1

Volume of cylinder=3 times volume of cone ----for an equal base cone, 3 times height, or for an equal height, 3 times base. The other cylinder or cone is under.

V=h*r^2 // the rest are constants

If I have only 2 values to be used (positive) and I want the greatest volume I would place my biggest value in the variable that is squared.

This is a conceptual solution to suffice the question of which one has the larger volume. It's not really an exact numerical solution like the ones mentioned so far, but conceptually we can look at it from the perspective of which one is closer to a sphere . Given the same surface area, a sphere is a shape that has the largest possible volume . Since these two have same surface volume, one that is closer to a spherical shape will have the larger volume.

Consider a rectangle with side lengths of $h$ and $w$ , where $h > w$

Using the formula $C = 2\pi r$ and $V = \pi*height*radius^{2}$ , if we roll the rectangle with $h$ as the height of the cylinder, we get volume $V = (h)(\frac{w}{2*\pi})^{2}(\pi) = \frac{w(hw)}{4\pi}$

Likewise, if we roll the rectangle with $w$ as the height of the cylinder, we get $V = (w)(\frac{h}{2*\pi})^{2}(\pi) = \frac{h(hw)}{4\pi}$

From the inequality constraint mentioned earlier $h > w \implies \frac{h(hw)}{4\pi} > \frac{w(hw)}{4\pi}$

Therefore, the cylinder formed from taking the width as the height will always have larger volume.

All I know is that when you find the volume of the cylinder squaring the larger number will give me the larger volume and the short one has a larger radius

Simple, if you that a 330 ml coca-cola cane pretty much maximizes the volume:area ratio. The larger and shorter cylindrer looks more like a cola-cola cane than the slimmer and taller one.

the long one got around 1042 and the short one 1474.

Those dimensions are of ISO standard A4 paper.

Off topic: ISO standard A0 is defined as paper that has 1sq.M. area and has aspect ratio of 1:sqrt(2). Which is necessary for their folding property (2x A4 = A3, 2xA3=A2...)

To be honest, I don't know much about math. I just assumed that their surfaces on the sides were the same (the sheet of paper), but the short and fat one has more surface on the top and bottom, so maybe that means it has more volume?

Lets keep this simple. Calculating the volume of the cylinder will involve one of the values being part of a calculation that is increased by a square factor. To maximize the volume, choose the larger value to be involved in that part of the calculation.

Since, Volume of Cylinder=2πr^2h The Volume get highest increment depending upon r (radius). Since the fat one has larger radius it will have more volume too.