min ( D E + E F ) = ?
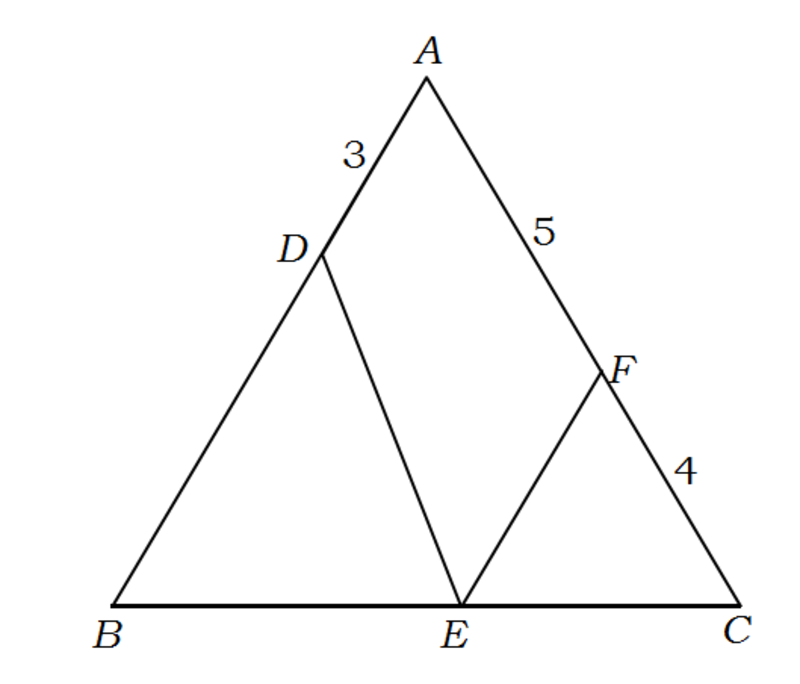
Triangle A B C is equilateral. Point D on A B and F on A C are such that A D = 3 , A F = 5 , and F C = 4 . E is a point on B C . Find the minimum length of D E + E F .
The answer is 9.53939.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let ∣ B E ∣ = a , position coordinates of A , B , C , E be ( 2 9 , 2 9 3 ) , ( 0 , 0 ) , ( 9 , 0 ) , ( a , 0 ) respectively. Then those of D and F are ( 3 , 3 3 ) and ( 7 , 2 3 ) respectively. So ∣ D E ∣ = ( 3 − a ) 2 + 2 7 and ∣ E F ∣ = ( 7 − a ) 2 + 1 2 .
∣ D E ∣ + ∣ E F ∣ = ( 3 − a ) 2 + 2 7 + ( 7 − a ) 2 + 1 2 is optimum when it's first derivative with respect to a is zero, that is, 5 a 2 − 1 0 2 a + 4 0 5 = 0 ⟹ a = 1 5 and a = 5 . 4 . For a = 1 5 , the sum is ≈ 2 1 . 7 9 4 5 . For a = 5 . 4 , the sum is ≈ 9 . 5 3 9 3 9 . So the minimum value of the sum is ≈ 9 . 5 3 9 3 9 .
The shortest path is one traveled by light . So we can treat B C as a mirror, if D E and E F are the incident and reflected beams respectively, then the angle of incident is equal to the angle of refection. We note that D ′ E , the image of D E , and E F is a straight line. Then the minimum D E + E F = D ′ E + E F = F G 2 + D ′ G 2 .
Since △ A B C is equilateral, we can work out it has a side length of 9 , and H I = F G = 4 , D H = 3 3 , and F I = 2 3 . We also note that F G = D H + F I = 5 3 . Then min ( D E + E F ) = 4 2 + ( 5 3 ) 2 ≈ 9 . 5 4 .