ABC problem?

The Cosine Rule $a^2 \; = \; b^2 + c^2 - 2bc\cos A \hspace{2cm} c^2 \; = \; a^2 + b^2 -2ab\cos C$ together with the given condition $a^2 - c^2 \,=\, bc$ tells us that $b \; = \; c(1 + 2\cos A) \hspace{2cm} \cos C \; = \; \frac{b+c}{2a}$ Putting these two statements together, and using the Sine Rule, we have $\begin{aligned} \cos C & = \; \frac{c(1 + \cos A)}{a} \; = \; \frac{\sin C(1 + \cos A)}{\sin A} \\ \sin A \cos C - \cos A \sin C & = \; \sin C \\ \sin(A-C) & = \; \sin C \end{aligned}$ Since $A,C$ are angles in a triangle, we deduce that $A-C=C$ , so that $A=2C$ , and hence $C = \tfrac13(\pi-B) =\tfrac13(\pi-\theta)$ . Thus the answer is $1+1+3=\boxed{5}$ .

Let $\angle BCA=x$ . As shown below, we consider a circle of radius $AB$ centred at $B$ . Suppose this circle intersects $BC$ at two points $E$ and $F$ :

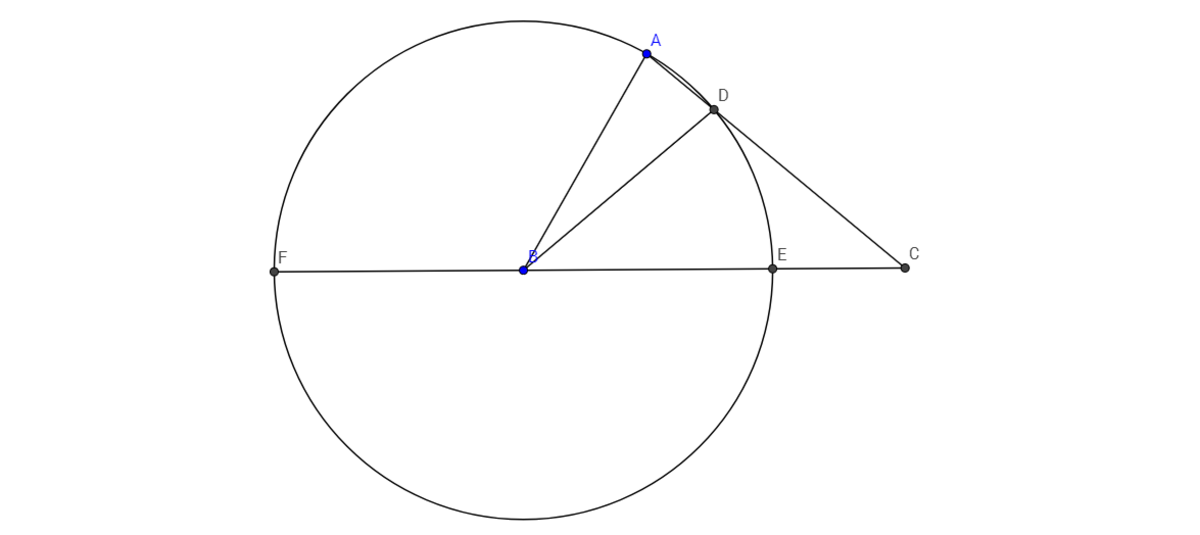
Note that $AB \times AC=BC^2-AB^2$ can be rewritten as:

$AB \times AC=(BC-AB)(BC+AB)$

Considering that $AB=BE$ as both represent the radius of the circle,

$AB \times AC=(BC-BE)(BC+BE)$

$AB \times AC=CE \times CF$

Now employing the properties of circles,

$CD \times AC=CE \times CF$ as the two lines from point $C$ intersect the circle at $A$ , $D$ , $E$ and $F$ . It then follows that $AB=CD$ . Consdering that $AB=BD$ , this means that $BD=CD$ and hence $\angle CBD=\angle BCD=x$ .

Then $\angle ADB=\angle CBD+\angle BCD=x+x=(1+1)x=2x$ .

Next $AB=BD$ as both represent the radius of the circle so $\angle BAD=\angle ADB=2x$ .

Finally,

$\angle BAC+\angle BCA+\angle ABC=\pi$

$2x+x+\theta=\pi$

$(2+1)x=\pi-\theta$

$3x=\pi-\theta$

$x=\frac{\pi-\theta}{3}$

Therefore, $p=1$ , $q=1$ and $r=3$ which means $p+q+r=\boxed{5}$ as required.