Hitting a square dartboard

Probability Level 2

ABCD is a square shaped board. 4 equal rectangles are drawn into it. The length of the sides of the rectangles are x x and y y where x / y = 3 x/y = 3 . Rahat throw a dart to the board. If the probability of the dart hitting the black portion is a / b a/b where a , b a, b are coprime positive integers, then find a + b a + b .


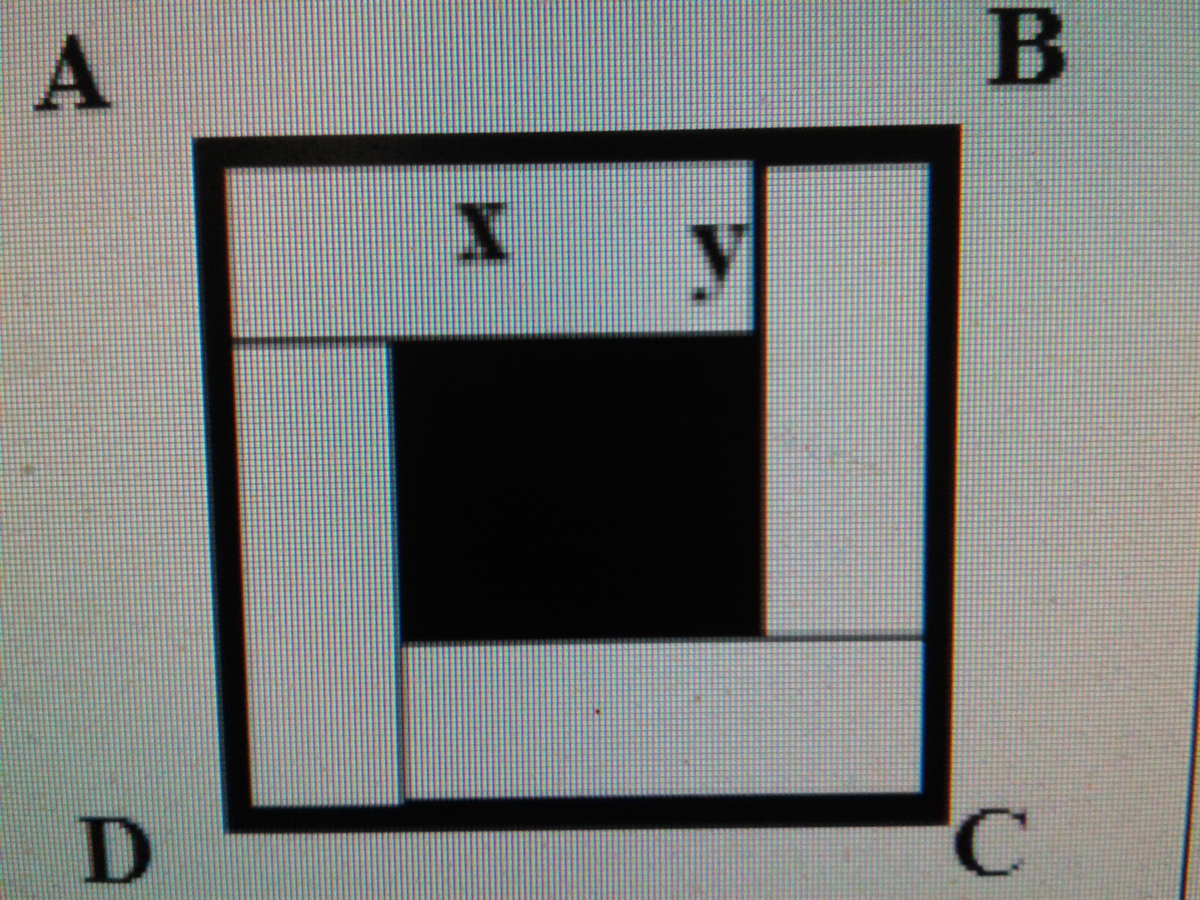
The answer is 5.

Akash Hossain by Akash Hossain , 18, Bangladesh

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Given x y \frac{x}{y} = = 1 3 \frac{1}{3} , we realize that:

The side of the bigger square = = 4 y 4y and the black figure thus formed is a square with each side = = 2 y 2y

So, P ( Hitting the black figure ) = A r . I n n e r S q u a r e A r . A B C D = ( 2 y ) 2 ( 4 y ) 2 = 1 4 P(\text{Hitting the black figure}) = \frac{Ar. Inner Square}{Ar. ABCD} = \frac{(2y)^{2}}{(4y)^{2}} = \frac{1}{4}

Hence, the solution sought = 1 + 4 = 5 = 1 + 4 = \boxed{5}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

But what will be the explanation of using area in counting the probability?

Akash Hossain - 3 years, 4 months ago

Log in to reply

Area of ABCD denotes all possible outcomes - all the points the dart can hit will be confined within ABCD.

Area of inner square denotes all favourable outcomes - all the points the dart needs to hit will be confined within this inner square.

A Former Brilliant Member - 3 years, 4 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...