Regular Partitioning
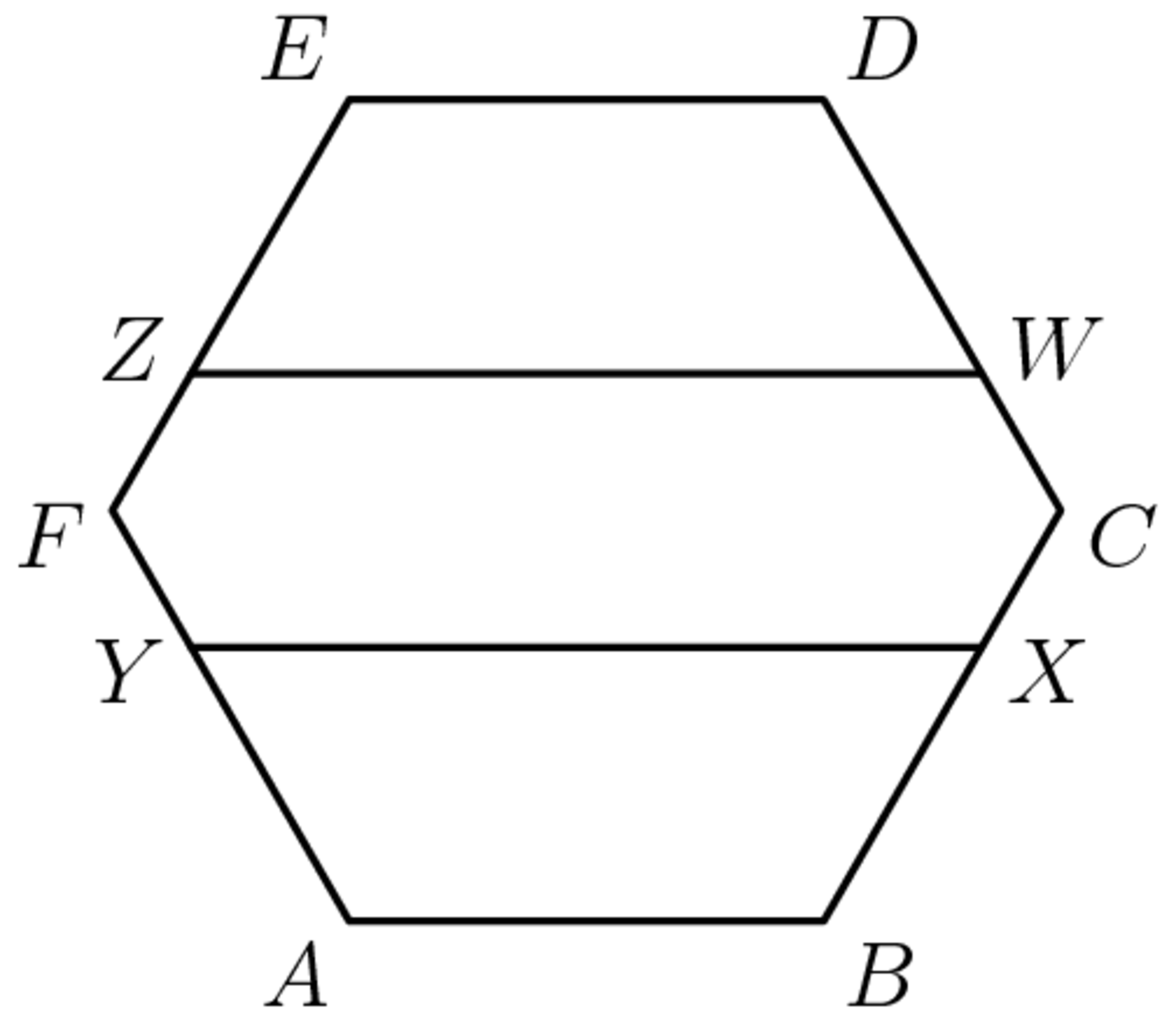
In a regular hexagon , points , , , and are on sides , , , and , respectively, in a way such that , , , and are parallel and equidistant. If the side length of is 1, what is the area of hexagon ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
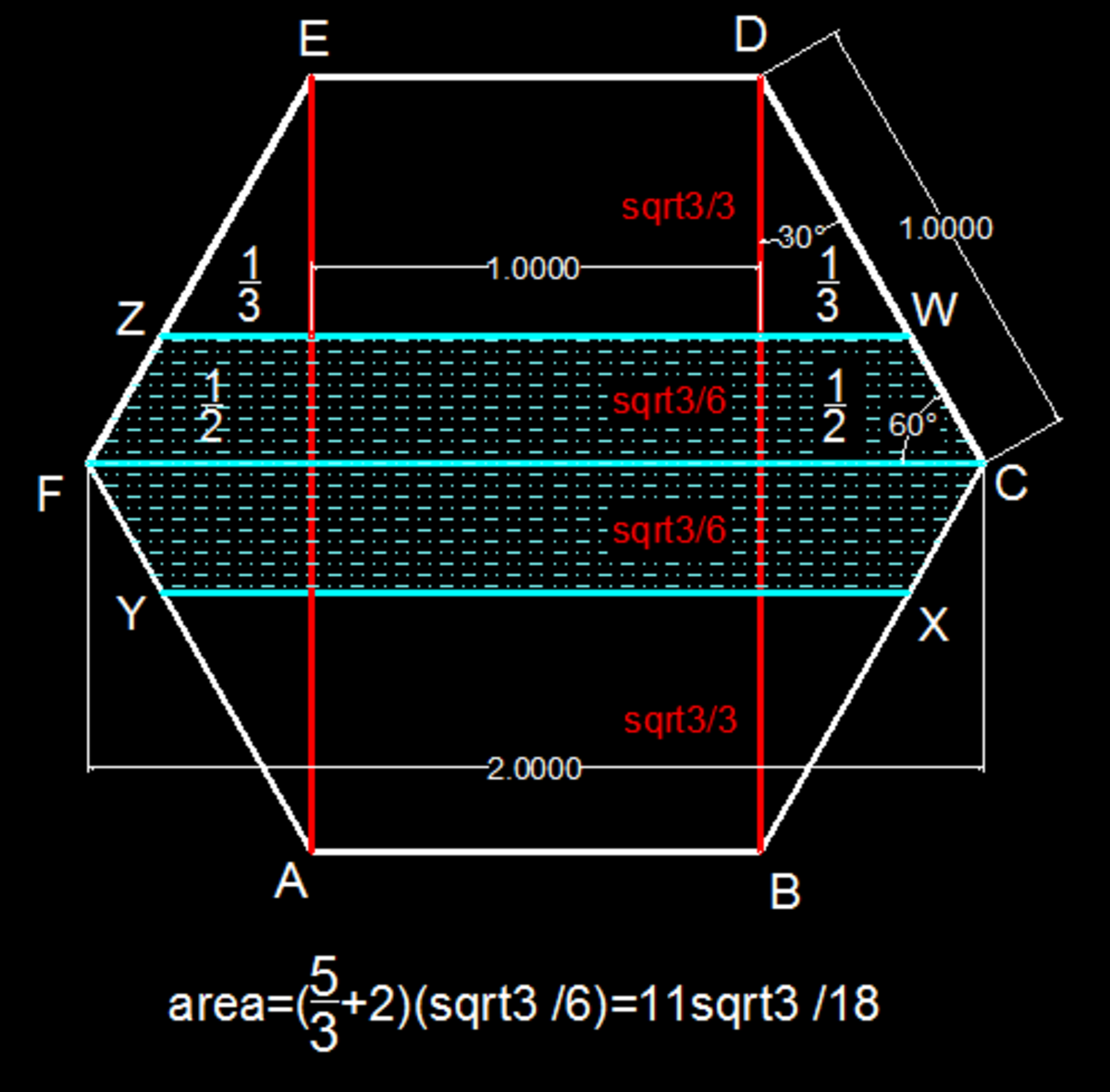
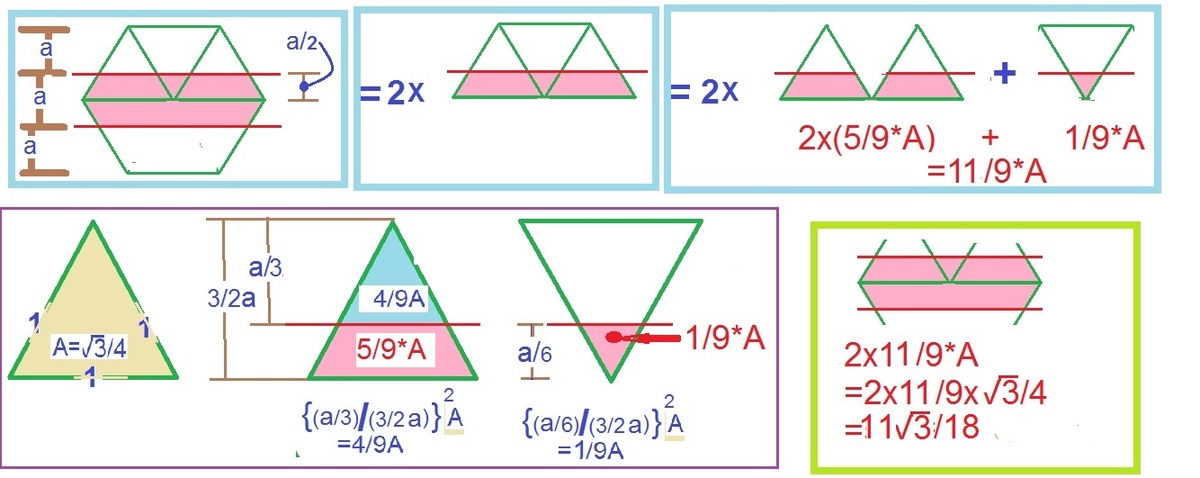
We draw equilateral triangles as shown above. We can split up W C X Y F Z into two trapezoids. B D = 3 (since it is twice the altitude of an equilateral triangle with side length 1 ).
Zoom into the top half of A B C D E F :
The smaller equilateral triangle is similar to the larger ones. We are given that A B , W Z , X Y , and E D are parallel and equidistant, so they divide A B C D E F (and therefore B D ) into thirds. So, the altitude of the larger equilateral triangles is 3 3 , and the altitude of the smaller equilateral triangle is 6 3 . From that, we know that the smaller equilateral triangle is similar to the larger ones with a similarity ratio of 1 : 2 .
The base of the smaller equilateral triangle is 3 1 (because of 30-60-90 triangle ratios). Since the similarity ratio between the smaller and larger equilateral triangles is 1 : 2 , the larger ones each have bases of 3 2 . Therefore, Z W = 3 5 . Since we know the height ( 6 3 ) and two bases of trapezoid Z W C F (since F C = 2 ) we can compute its area to be 3 6 1 1 3 .
Since W C X Y F Z is made up of two of these trapezoids, its area is 2 ⋅ 3 6 1 1 3 = 1 8 1 1 3 .