This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
pisello nerissimo di vinicio moltiplicando il pisellone del sigarone
Log in to reply
sono bello sono fresho sono un bello figo gu pezzo di merda bastardoooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooo
SARA MANZONE CULO
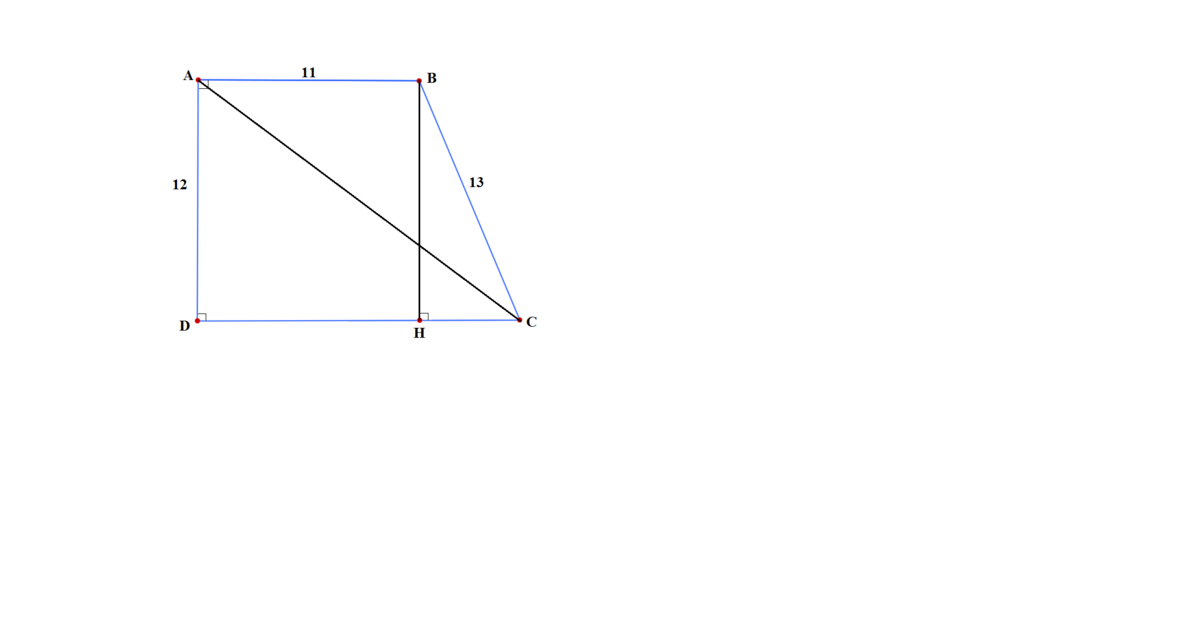
how do you get 5cm from letters? please explain. I'm confused.
Log in to reply
You apply pythagorean theorem Consult the wiki page.
They create a triangle where one side and the hypothenuse is known (if the line between points B and H is paralell to the line between A and D they are the same length, which is 12cm). Knowing the hypothenuse and one of the sides they can use the pythagorean theoriem a^2 + b^2 = c^2 and get that the remaining side has to be equal to the square root of 169 - 144 which is 5cm.
Since the line between D and C is parallell with the line between A and B The line between D and H must also be 11cm add the 5 cm for the line between H and C and you have a line that is 16cm. Then they use the pythagorean theorem again on the triangle made up of the lines between A and D, between D and C and finally between C and A. Here they see that the squares of the sides adds up to 400 (144 + 256 = 400). The squareroot of 400 is 20, thus the hypothenuse is 20cm.
To solve this problem, I guessed and checked. I don't understand what the formula is to solve this problem. I would rate this problem a 5 because I feel pretty neutral about it. I felt a bit clueless while solving this problem but I think that since we are doing a geometry unit in math, we might learn about this.
Log in to reply
The formula is simply Pythagorean Theorem (you should definitely know this if you want to do geometry problems). Check the Brilliant wiki
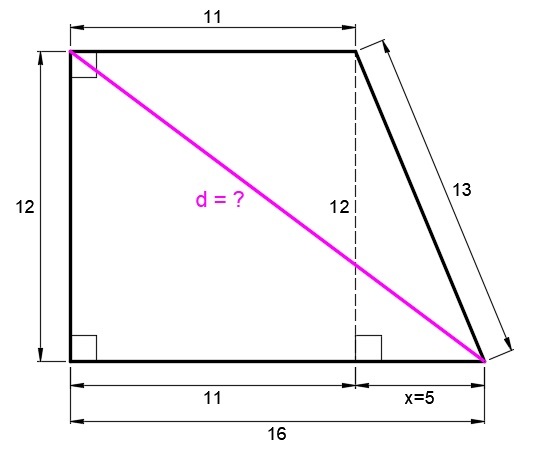
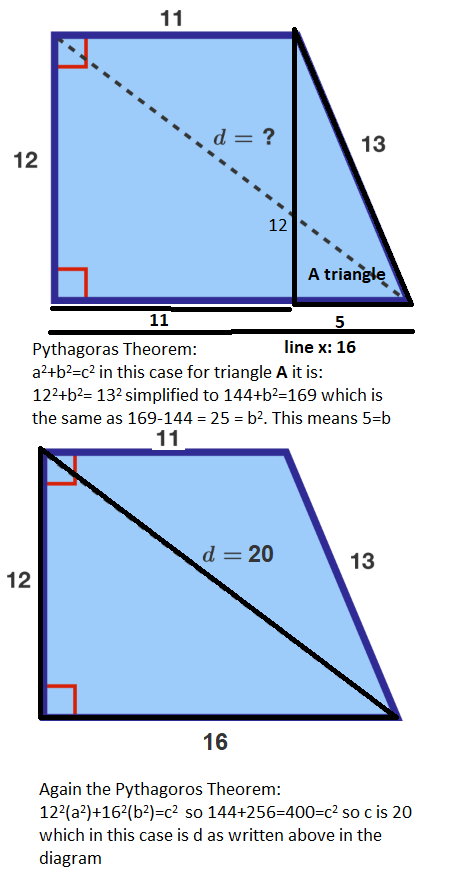
Consider my diagram. First, draw the dashed line as shown. We have now a rectangle and a small triangle and a big triangle. Find the unknown x in the small triangle by using pythagorean theorem, we have
x = 1 3 2 − 1 2 2 = 5
So the legs of the big triangle are 1 2 and 1 1 + 5 = 1 6 .
By pythagorean theorem again, the unknown d (hypotenuse of the big triangle) is
d = 1 2 2 + 1 6 2 = 2 0
I'm a new member here and I would like to ask how do you make those beautiful drawings because I want to contribute my answer to more geometric questions, but I don't know how to draw it on the computer (what software are you using...?)
Log in to reply
I use the software autoCAD . It is a 2-D and 3-D computer-aided drafting software application used in architecture, construction, and manufacturing to assist in the preparation of blueprints and other engineering plans. It so happen that I have been using autoCAD so I used it in making my diagrams.
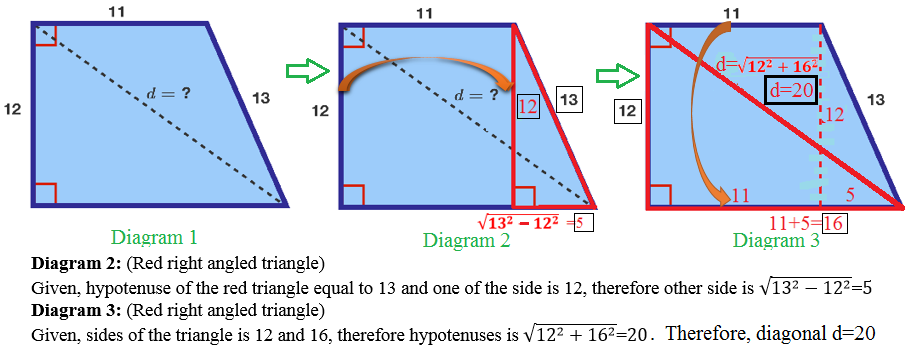
Actually, you have a rectangle and two right triangles.
+1 for actually mentioning the Pythagorean theorem :)
Relevant wiki: Pythagorean Theorem
Pythagoras' Theorem:
In a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
ABC form a triangle, and therefore AC is the hypotenuse. According to Pythagoras theorem A^2+B^2=C^2. the answer is 17.
Log in to reply
Please check the problem and solution again, the answer is not 17. What values you consider for A, B and C in the given problem to reach the solution 17.
Your answer applies only if the angle formed by AB and BC is a right angle.
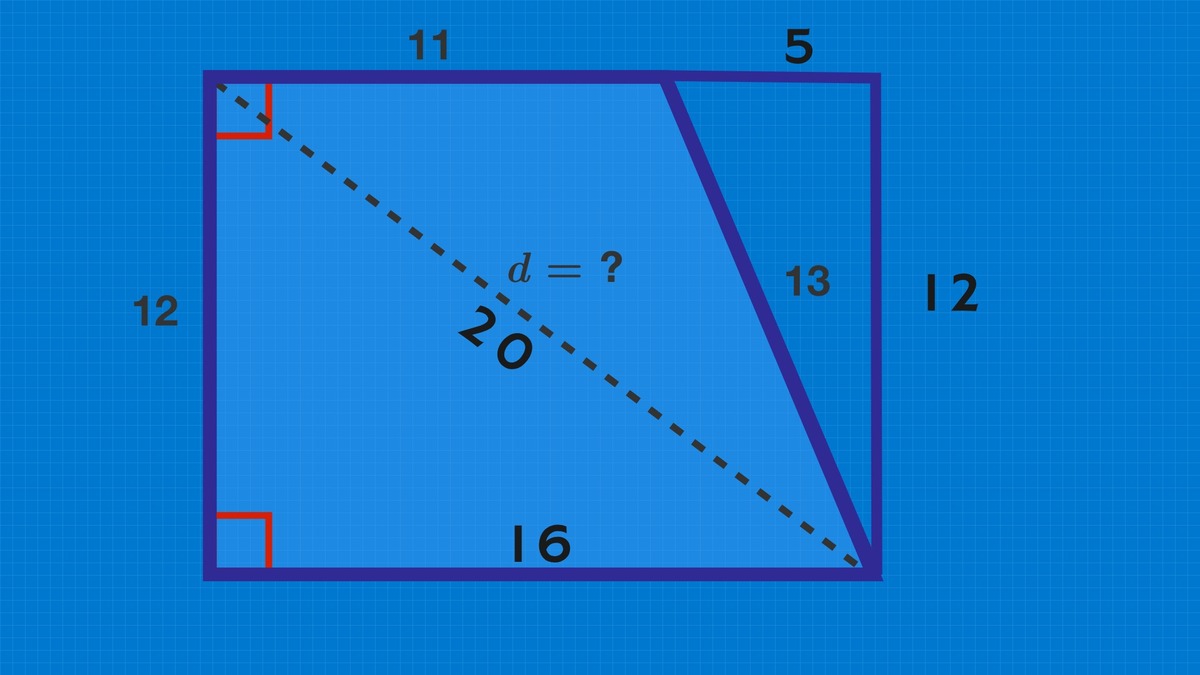
If we extent this figure to create a rectangle, we will get a new triangle in the top right with a hypotenuse of 13 and one leg which is 12. We can recognize this as a 5-12-13 triangle which tells us the length of the other leg is 5. We can now use the Pythagorean Theorem to solve for d 1 2 2 + 1 6 2 = d 2 d = 2 0
Since the Quadrilateral's sides are not equal but only two sides being right angles, Taking out the part 11 x 12 First thing you have to find the extra part dimensions ( a right angle triangle with the hypotenuse 13 and height 11, the width will be 5, add this triangle as rotated 180 degrees to the upper right side of the quadrilateral - hat will make the shape perfect square -, now split the square from center by the line "d" you will have a right angled triangle with the dimensions 16 x 12. Next step is applying Pythagorean theorem to the triangle to find the hypotenuse and BOOM d=20
The diagnoal side of the quadrilateral is the long side of a pythagorean triangle and measures 13 units. We know the the longer of the other two sides measures 12 units. Thus the width of this triangle is 5cm. This means that the diagonal we are being asked to calculate is effectively the long diagonal of a 16 x 12 rectangle, or the hyopteneuse of a right-angle triangle whiose shorter sides are 12 and 16. Thus it is equal to the square root of ((12 x 12) + (16 x 16)) = the square root of (256 + 144) = the square root of 400 = 20.
Using Vector addition.
we take the top side(line) to be the vector A=(11,0), then we take the vector B of magnitude 13 to be B=(13cos(theta), 12); we add x and y components together and square root the the squares i.e. sqrt( (added x)^2+(added y)^2 )
note: some geometry similar to other answers is used to obtain the angle theta.
d = 1 2 2 + ( 1 1 + 1 3 2 − 1 2 2 ) 2 = 1 4 4 + ( 1 1 + 1 6 9 − 1 4 4 ) 2 = 1 4 4 + ( 1 1 + 2 5 ) 2 = 1 4 4 + ( 1 1 + 5 ) 2 = 1 4 4 + 1 6 2 = 1 4 4 + 2 5 6 = 4 0 0 = 2 0
If you allow for the base to be shorter than the top side then there is a second solution. Following the same logic as other solutions and dropping a 5,12,13 triangle down we get the base is 11-5=6 and by pythagoras d=6×sqrt(5)
We can make a right triangle where we use the side of length 13 as its hypotenuse. The height of this right triangle (with hypotenuse of length 13) is parallel and equal to the side with length of 12. Thus its other side is 5. Looking back at the whole picture of the trapezoid, the other base is equal to 11+5 (the given base and the base of the right triangle of hypotenuse length of 13) which is 16. We can now have the larger right triangle, where we can use 16 as its base, 12 (as given) as its height, and "d" (the diagonal of the trapezoid that we are looking for) as its hypotenuse. We can now use again the Pythagorean Theorem using the given, to find d. 12^2 +16^2 =d^2 . so we have 144+256=d^2 400=d^2 20=d
Extend the 12cm width to the 13cm side. This makes an extra triangle.
Use 180-arcsin(12/13) to then get the angle at the top right of the trapezium. It would be 112.6 degrees.
Then use Cosine rule: c^2= a^2 + b^2 - 2ab*cos(112.16)
c^2 = 400
c = 20.
This makes the length of the diagonal "d" 20cm.
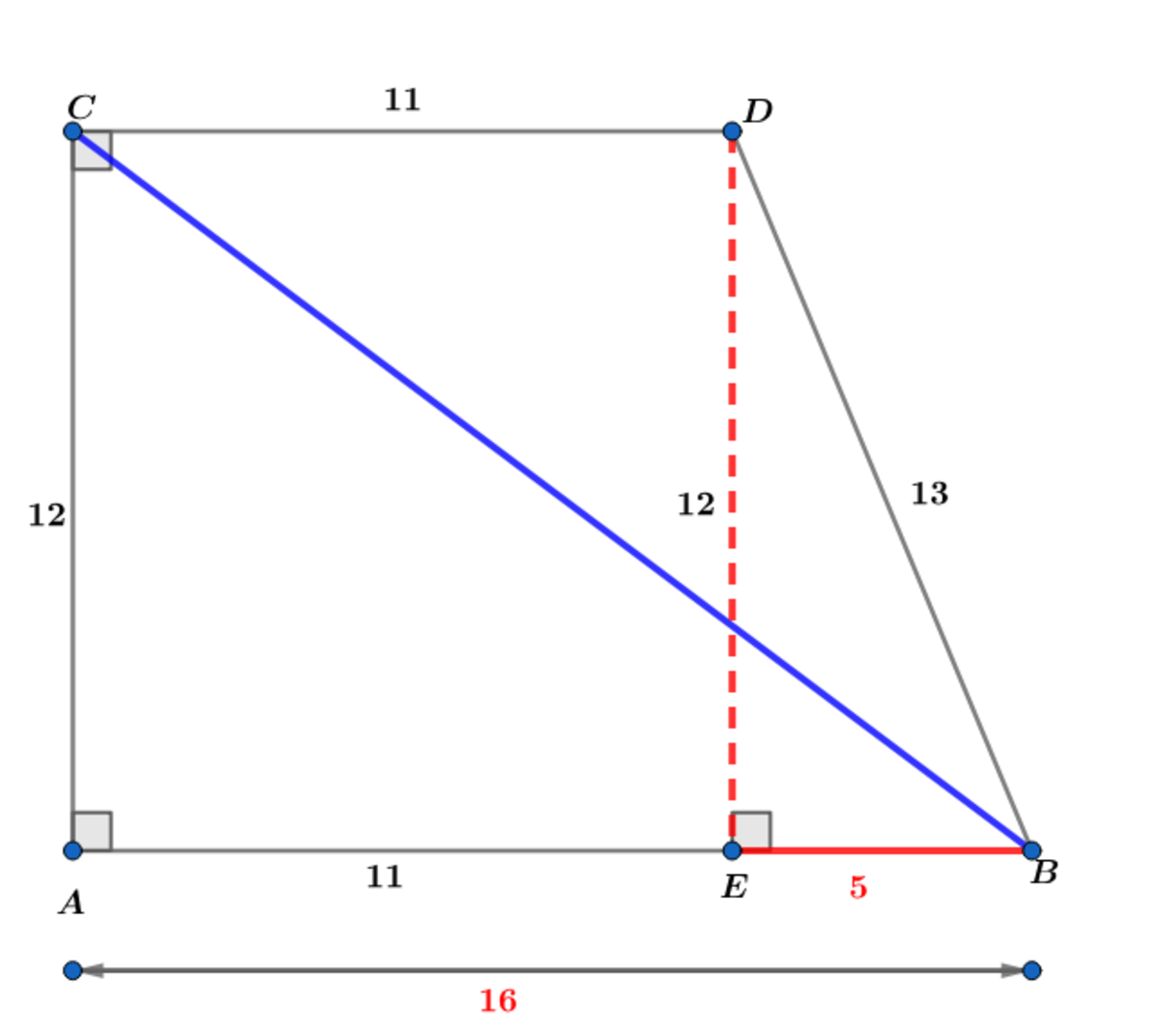
△ D E B is a ( 5 , 1 2 , 1 3 ) right triangle and △ A C B is a ( 3 ∗ 4 , 4 ∗ 4 , 5 ∗ 4 ) = ( 1 2 , 1 6 , 2 0 ) right triangle ∴ B C = 2 0 .
BH is perpendicular to DC.
BH = 12 cm.
In △ BHC, BC^2 = BH^2 + HC^2 so HC = 5 cm.
therefore DC = 16 cm.
In △ ADC, AC^2 = AD^2 + DC^2 so AC = 20 cm.