Absolute-ly Ab-salute

$1+2+3+...+20=\frac{20\times21}{2}=210$

$1+2+3+...+14=\frac{14\times15}{2}=105$

$15+16+17+...+20=210-105=105$

So, $(1+2+3+...+14)-(15+16+17+...+20)=0$

The above calcution is useful indeed as by algebraic manipulation:

$f(x)=|x-1^{3}|+|2x-2^{3}|+|3x-3^{3}|+...+|19x-19^{3}|+|20x-20^{3}|=|x-1^{3}|+|2x-2^{3}|+|3x-3^{3}|+...+|14x-14^{3}|+|15^{3}-15x|+...+|19^{3}-19x|+|20^{3}-20x|\geq|x-1^{3}+2x-2^{3}+3x-3^{3}+...+14x-14^{3}+15^{3}-15x+...+19^{3}-19x+20^{3}-20x|=0+20^3+19^3+18^3+...+15^3-14^3-13^3-12^3-2^3-1^3=(20^3+19^3+18^3+...+2^3+1^3)-2\times(14^3+13^3+12^3+...+2^3+1^3)=(\frac{20\times21}{2})^{2}-2\times(\frac{14\times15}{2})^{2}=210^{2}-2\times105^{2}=2^2\times105^2-2\times105^2=2\times105^{2}$

The zero-points of each absolute term $|x-1^3|$ , $|2x-2^3|$ , $|3x-3^3|$ , $\ldots$ , $|20x-20^3|$ are $x=1^2$ , $x=2^2$ , $x=3^2$ , $\ldots$ , $x=20^2$ respectively, thus if we continuously crank $x$ from $-\infty$ to $\infty$ , the signs of $|x-1^3|$ , $|2x-2^3|$ , $|3x-3^3|$ , $\ldots$ , $|20x-20^3|$ all start at negative and will take turns become positive (i.e. first the sign of $|x-1^3|$ becomes positive when we crank $x$ past $1^2$ , then followed by $|2x-2^3|$ past $x=2^2$ , then $|3x-3^3|$ etc.)

Plot a "derivative table":

$\begin{array}{|c|c|c|c|c|c|c|c|} \hline \\ & \dfrac{d}{dx}|x-1^3| & \dfrac{d}{dx}|2x-2^3| & \dfrac{d}{dx}|3x-3^3| & \ldots & \dfrac{d}{dx}|19x-19^3| & \dfrac{d}{dx}|20x-20^3| & \dfrac{d}{dx}f(x) \\ \hline x<1^2 & -1 & -2 & -3 & \ldots & -19 & -20 & -210 \\ \hline 1^2\leqslant x<2^2 & \color{#20A900}+1 & -2 & -3 & \ldots & -19 & -20 & -208 \\ \hline 2^2\leqslant x<3^2 & \color{#20A900}+1 & \color{#20A900}+2 & -3 & \ldots & -19 & -20 & -204 \\ \hline 3^2\leqslant x<4^2 & \color{#20A900}+1 & \color{#20A900}+2 & \color{#20A900}+3 & \ldots & -19 & -20 & -198 \\ \hline \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ \hline 19^2\leqslant x<20^2 & \color{#20A900}+1 & \color{#20A900}+2 & \color{#20A900}+3 & \ldots & \color{#20A900}+19 & -20 & 170 \\ \hline 20^2\leqslant x & \color{#20A900}+1 & \color{#20A900}+2 & \color{#20A900}+3 & \ldots & \color{#20A900}+19 & \color{#20A900}+20 & 210 \\ \hline \end{array}$

Where $f'(x)=\dfrac{d}{dx}f(x)$ is the sum of the derivatives of all the absolute terms, which for $n^2\leqslant x<(n+1)^2$ , $1\leqslant n\leqslant19$ , can be computed with $\displaystyle \dfrac{d}{dx}f(x)=2\sum_{i=1}^ni-\sum_{i=1}^{20}i=n(n+1)-210$

Notice that $f'(x)$ starts out at negative and increases at intervals as $x$ increases, we can estimate that the shape of the graph of $f(x)$ looks something like this:

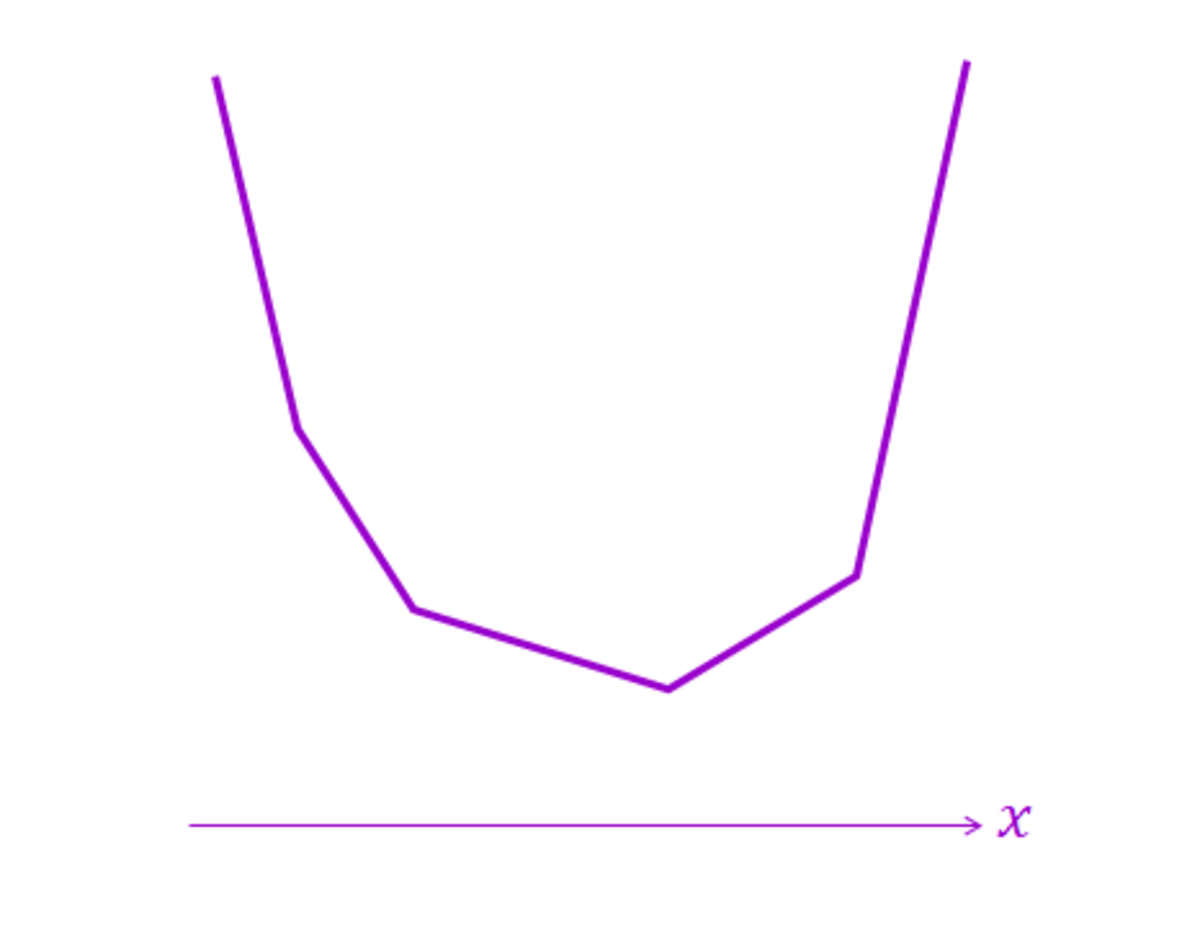
To find the minimum value of $f(x)$ , our target is to make $f'(x)$ as close to 0 as possible .

Turns out it's possible for $f'(x)$ to be equal to 0, if we solve for $f'(x)=0$ : $n(n+1)-210=0$ $n^2+n-210=0$ $\therefore n=14 \quad(n>0)$

Hence, $14^2\leqslant x<15^2$ is when the minimum of $f(x)$ occurs, when $14\leqslant x<15$ : $\begin{aligned}f(x)&=(x-1^3)+(2x-2^3)+(3x-3^3)+\ldots+(14x-14^3)-(15x-15^3)-\ldots-(20x-20^3) \\ &=-1^3-2^3-3^3-\ldots-14^3+15^3+\ldots+20^3 \\ &=\left[\frac{20\times21}{2}\right]^2-2\left[\frac{14\times15}{2}\right]^2 \\ &=22050 \end{aligned}$ (the $x$ terms all cancel out since $f'(x)=0$ ) $\therefore 2a^2=22050$ $a=105$