Absolute Value Has a Team
 Find the greatest natural number
n
for which the following equation holds :
∣
i
+
2
i
2
+
3
i
3
+
.
.
.
.
.
+
n
i
n
∣
=
1
8
2
Find the greatest natural number
n
for which the following equation holds :
∣
i
+
2
i
2
+
3
i
3
+
.
.
.
.
.
+
n
i
n
∣
=
1
8
2
Details and Assumptions :
i 2 = − 1
Practice the set Target JEE_Advanced - 2015 and boost up your preparation.
Image Credit: Wikimedia Complex Number Illustration
The answer is 36.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
equation is of the form |(1-3+5-7...)i+(-2+4-6+8...)|= 18 2
Case(1) n=4r
Equation becomes |(1-3+5-7... 2r terms)i+(-2+4-6+8... 2r terms)|=18 2
⇒ |((-2)+(-2)+... r terms)i +(2+2+... r terms)|=18 2
⇒ |(-2r)i+(2r)|=18 2
⇒ r=9 (Taking only +ve value as we want maximum)
n=36
Case(2) n=4r+1
Equation becomes |(2r+1)i+(2r)|=18 2
Which is not possible as LHS is o d d while RHS is e v e n
Case(3) n=4r+2
Equation becomes |(2r+1)i+(-2r-2)|=18 2
Not possible like Case(2)
Case(4) n=4r+3
Equation becomes |(-2r-2)i+(-2r-2)|=18 2
⇒ r=8 (Taking only +ve value as we want maximum)
n=35
Three cases: Case 1: There are a multiple of 4 number of terms on LHS. Grouping in groups of 4 gives (i-2-3i+4)+(5i-6-7i+8)+.....=(2-2i)+(2-2i)+(2-2i)+....=n/2-n/2i for every n that is a multiple of 4. Magn(n/2-n/2i)=√2n/2=18√2, n=36. Case 2: A multiple of 4 plus 2 terms. By a similar argument, after applying the magnitude formula, the equation is disproved in all integers. Similar argument for Case 3: A multiple of 2 plus one term.
The sequence is an AGP - Arithmetico-Geometric progression. Where a = 1 , d = 1 , r = i . So sum to n terms of AGP = 1 8 2
Multiply the differentiation of GP [ x + x 2 + x 3 . . . . . by x yields [ x + 2 x 2 + 3 x 3 . . . . . ] . Use it and put x=i and simplify it.
18 ( (2)^ (1/2) ) may be written as ( 18^2 + 18^2 )^( 1/2 ). thus for the L.H.S we have x + iy = 18 ((2) ^ (1/2)). where x= 18 and y=18. ( remember that since only integers are used in LHS therefore the modulus must be equal to the the sum of perfect squares. and the coefficients of the real and complex part both must be integers ). See the trend:- for n=4, Z=2-2i ..... for n= 8: Z=4-4i ... thus we may conclude that for z to be equal to 18(2^(1/2)) we must have n= 36.
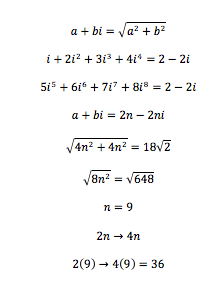
We can rewrite the terms in ∣ m o d u l u s ∣ as follows
( 4 + 8 + 1 2 + 1 6 . . . . ) − ( 2 + 6 + 1 0 + . . . ) + i ( ( 1 + 5 + 9 . . . ) − ( 3 + 7 + 1 1 + 1 3 . . . ) )
which is same as ( 2 + 2 + 2 + . . . . . ) − i ( 2 + 2 + 2 + ; . . ) there might however be some residual terms that will not cancel at the end,
with some hindsight, we can conclude that 1 8 2 is obtained for maximum n at x=y=18,
so we need 9 × 2 on either side,
If we assume n = 4 r then there are r terms on either half of equation,
as r = 9 , so 4 r = 3 6
so answer is n = 3 6
I couldnt find a better way, i admit that it is very slightly guess work