Absolute value polynomial
Algebra
Level
2
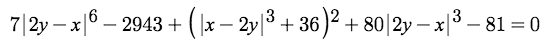
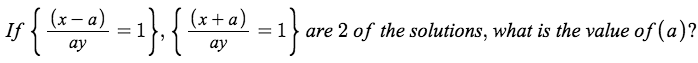
Hint: Group the 1st, 2nd, and 4th term :).
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since absolute value is positive even if what is inside the absolute value brackets is negative, and 2 y − x = − ( x − 2 y ) , we can convert all the ( 2 y − x ) into ( x − 2 y ) . Then, group the 1st, 2nd, and 4th term to form a quadratic and the 3rd and 5th term to form a difference of squares . Let a = ∣ x − 2 y ∣ 3 to make the math easier. The quadratic can be factored into ( 7 a − 1 0 9 ) ( a + 2 7 ) and the difference of squares into ( a + 4 5 ) ( a + 2 7 ) . An ( a + 2 7 ) can be factored out, leaving ( a + 2 7 ) ( 8 a − 6 4 ) . Since a represents a cube, ∣ x − 2 y ∣ 3 can be substituted back into the equation. Next, the Cube Sum and Difference formulas can be applied to get a product of two binomials and two trinomials. The Zero-Product Property can be applied here. Since absolute value cannot be negative, this eliminates one of the binomials. Also, the two trinomials have no solutions, which leaves us with ( ∣ x − 2 y ∣ ) = 2 . This can be split into x − 2 y = 2 and x − 2 y = − 2 , and by adding 2 y , subtracting 2 for the 1st equation and − 2 for the second equation, and dividing both sides by 2 y , we can obtain that a = 2 . As a result, a = 2 is the final answer.