An algebra problem by Rishabh Mishra
Algebra
Level
4
what is the minimum value of the expression
......
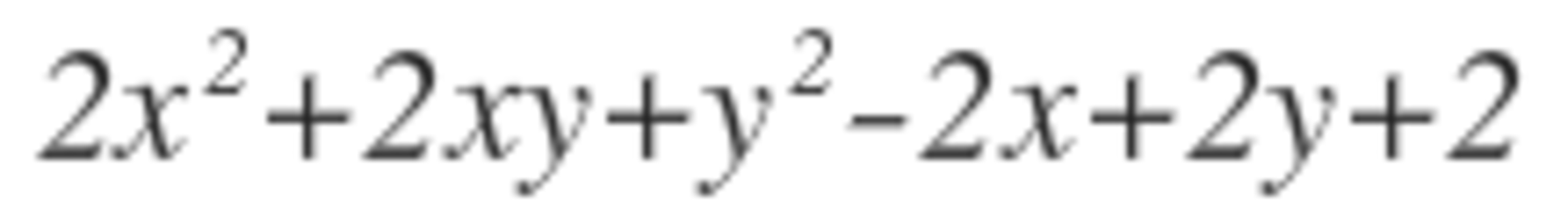The answer is -3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Differentiate the function partially w.r.t 'x' which leads to the following equation: 4x+2y-2=0........................................(1) Similarly partially differentiate the function w.r.t 'y' which leads to the equation: 2x+2y+2=0......................................(2) Solving above equations (1) & (2), we get x=2 y=-3
Again differentiate eq (1) w.r.t 'x' and if this value is greater than 0 then for x=2 ,the function has minimum value. Similarly differentiate eq(2) w.r.t 'y' and with the same principle mentioned above we can see that at y=-3 ,the function has minimum.
Hence the minimum value of function is obtained by substituting x=2 and y=-3 in the expression which leads to the value -3