Absolutely absolute
Solve the equation
∣ 2 x − 3 y ∣ + 7 x − 3 y − 1 3 = 0
Given that the value of x and the value of y can be expressed as b a and d c respectively and that they are both real, find the value of a + b + c + d
If you think that there are infinitely many rational solutions for x and y , input 0 as your answer.
If you think that there are no solutions for x and y , input − 1 as your answer.
The answer is 59.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
You should use the word non-negative instead of positive in your solution since 0 ∈ / R + , where R + denotes the set of positive real numbers.
The equation can be rewritten as follows:
∣ 2 x − 3 y ∣ = − 7 x − 3 y − 1 3
For all real x and y, it is obvious that L H S ≥ 0 and R H S ≤ 0
Therefore: L H S = R H S if and only if both equalities occur.
{ 2 x − 3 y = 0 7 x − 3 y − 1 3 = 0
{ x = 5 1 3 y = 1 5 2 6
Therefore, a + b + c + d = 2 6 + 1 5 + 1 3 + 5 = 5 9
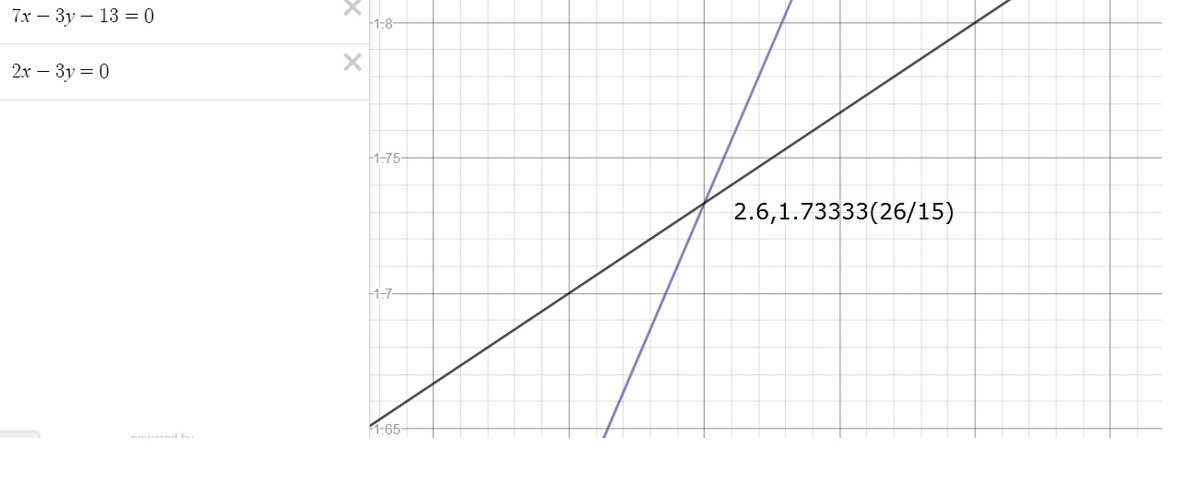
Notice that ∣ 2 x − 3 y ∣ is always positive and real and 7 x − 3 y − 1 3 is always non negative if it is real.
Since both sides are to be positive if x and y are real, then
2 x − 3 y = 0 7 x − 3 y − 1 3 = 0
Solving for these simultaneously gives
x = 5 1 3
y = 1 5 2 6
Therefore, a + b + c + d = 1 3 + 5 + 2 6 + 1 5 = 5 9