Absolutely interesting limit

Calculus Level 4

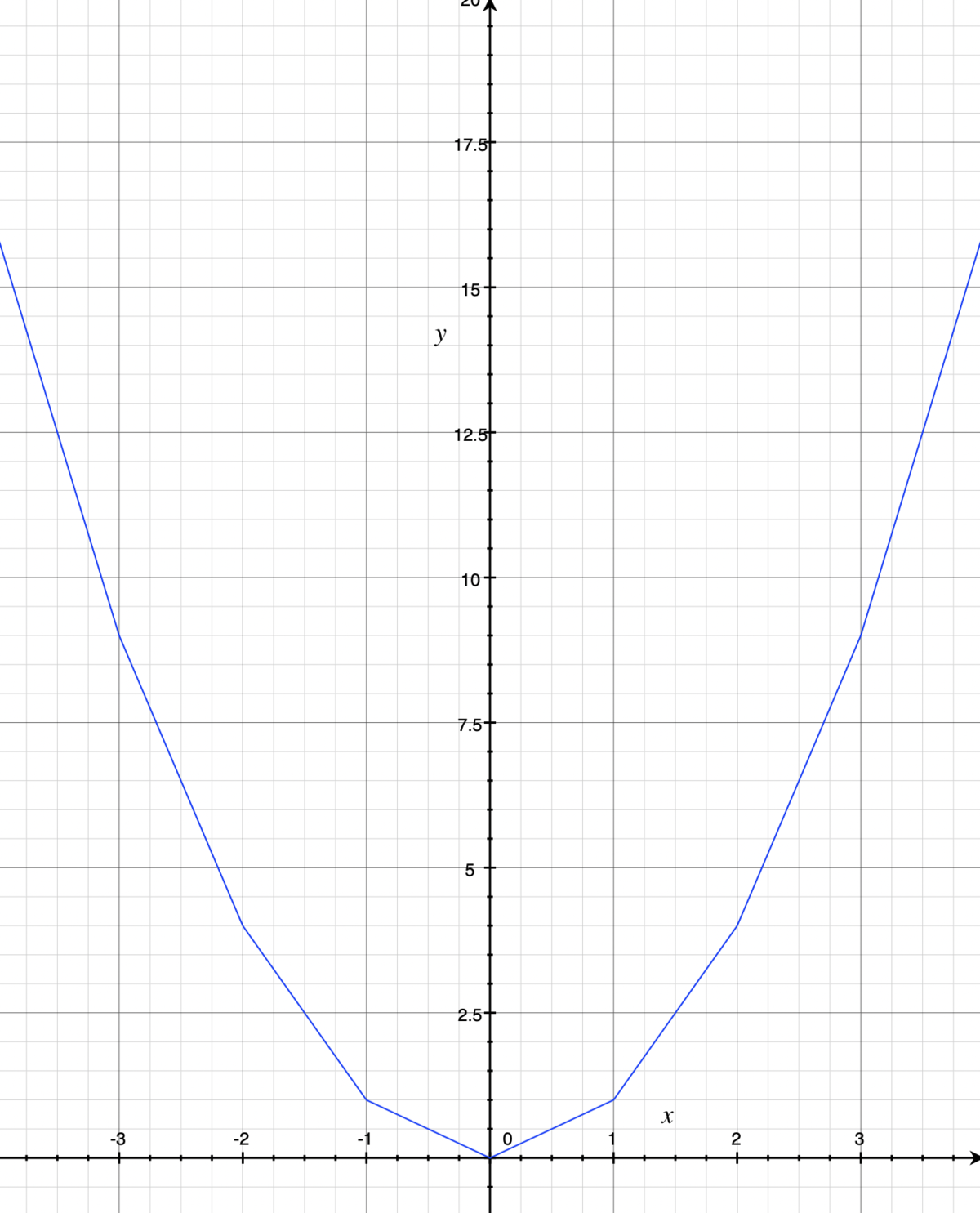
We can define a family of real functions g n g_n so that, for instance, g 3 ( x ) = ∣ x − 3 ∣ + ∣ x − 2 ∣ + ∣ x − 1 ∣ + ∣ x ∣ + ∣ x + 1 ∣ + ∣ x + 2 ∣ + ∣ x + 3 ∣ , g_3(x) = |x - 3| + |x - 2| + |x -1| + |x| + |x+1| + |x+2| + |x+3|, and more generally for integers n ≥ 0 n \geq 0 , g n ( x ) = ∑ k = − n n ∣ x + k ∣ . g_n(x) = \sum_{k = -n}^{n} |x + k|. Now let f ( x ) = lim ⁡ n → ∞ ( g n ( x ) − n ( n + 1 ) ) . f(x) = \lim_{n\to\infty} \left(g_n(x) - n(n+1)\right). Evaluate f ( 7.2 ) f(7.2) .

Hint : For integer values of x x , f ( x ) f(x) turns out to be a familiar function.


The answer is 52.

Arjen Vreugdenhil by Arjen Vreugdenhil , 44, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Arjen Vreugdenhil
Aug 29, 2020

It turns out that for integer values of x x , f ( x ) = x 2 f(x) = x^2 . You can easily check this with a few examples; I will also prove it below.

Also, each of the functions in the problem is piecewise linear; to be precise, linear on each interval [ k , k + 1 ] [k, k+1] between successive integers.

Thus the solution point lies on the line segment between ( 7 , 49 ) (7, 49) and ( 8 , 64 ) (8, 64) , which has a slope of 15. Thus f ( 7.2 ) = 49 + 0.2 × 15 = 52 f(7.2) = 49 + 0.2\times 15 = \boxed{52} .

Proof that f ( x ) = x 2 f(x) = x^2 for integer values of x x :

Let x x be an integer such that − n ≤ x ≤ n -n \leq x \leq n , g n ( x ) = ( n − x ) + ( n − x − 1 ) + ⋯ + 2 + 1 + 0 + 1 + 2 + ⋯ + ( n + x ) = ( 1 + 2 + ⋯ + ( n − x ) ) + ( 1 + 2 + ⋯ + ( n + x ) ) = 1 2 ( n − x ) ( n − x + 1 ) + 1 2 ( n + x ) ( n + x + 1 ) = 1 2 ( n 2 + x 2 − 2 n x + n − x ) + 1 2 ( n 2 + x 2 + 2 n x + n + x ) = n 2 + x 2 + n = x 2 + n ( n + 1 ) . \begin{aligned} g_n(x) & = (n-x) + (n-x-1) + \cdots + 2 + 1 + 0 + 1 + 2 + \cdots + (n+x) \\ & = \left(1 + 2 + \cdots + (n-x)\right) + \left(1 + 2 + \cdots + (n+x)\right) \\ & = \tfrac12(n-x)(n - x +1 ) + \tfrac12(n+x)(n+x+1) \\ & = \tfrac12(n^2 + x^2 - 2nx + n - x) + \tfrac12(n^2 + x^2 + 2nx + n + x) \\ & = n^2 + x^2 + n = x^2 + n(n+1). \end{aligned} Therefore, for all − n ≤ x ≤ n -n \leq x \leq n , g n ( x ) − n ( n + 1 ) = x 2 , g_n(x) - n(n+1) = x^2, and since by taking the limit we always accomplish n ≥ x n \geq x in the end, this means that f ( x ) = x 2 . f(x) = x^2.

2 Helpful 1 Interesting 5 Brilliant 0 Confused

There is no need for linear interpolation. f ( x ) = ( 2 ⌊ x ⌋ + 1 ) x − ⌊ x ⌋ ( ⌊ x ⌋ + 1 ) f(x) = (2 \lfloor x \rfloor + 1)x - \lfloor x \rfloor (\lfloor x \rfloor + 1)

Atomsky Jahid - 9 months, 2 weeks ago

Hello, I arrived at a different solution when solving this specific case. What I did was remove the absolute value as follows:

[ n − 7.2 ] + [ ( n − 1 ) − 7.2 ] + . . . + [ 9 − 7.2 ] + [ 8 − 7.2 ] + [ 7.2 − 7 ] + . . . + [ 7.2 − 1 ] + 7.2 + ∑ k = 1 n ( 7.2 + k ) [n-7.2]+[(n-1)-7.2]+...+[9-7.2]+[8-7.2]+[7.2-7]+...+[7.2-1]+7.2+\sum_{k=1}^{n}(7.2+k)

Here, we can clearly see that we can collect all the integers like this: n ( n + 1 ) − 28 n(n+1)-28 ; and, after some algebra, we will get 7.2 ( 15 ) 7.2(15) . With this in mind and without any rigorous proof, I intuitively arrived at the general formula f ( x ) = ( 2 ⌊ x ⌋ + 1 ) x − ⌊ x ⌋ ( ⌊ x ⌋ + 1 ) 2 f(x)=(2\lfloor{x}\rfloor+1)x-\dfrac{\lfloor{x}\rfloor(\lfloor{x}\rfloor+1)}{2} .

However, when doing a rigorous proof and checking the answers posted for this problem the formula is: f ( x ) = ( 2 ⌊ x ⌋ + 1 ) x − ⌊ x ⌋ ( ⌊ x ⌋ + 1 ) f(x)=(2\lfloor{x}\rfloor+1)x-\lfloor{x}\rfloor(\lfloor{x}\rfloor+1) . I have spent some time thinking about it but I can't wrap my head around it since I believe I didn't make any mistakes in my first solution, where the answer is 80 instead of 52.

Saúl Huerta - 9 months, 1 week ago

I think something goes wrong when you collect the integers. The first few terms (up to [ 8 − 7.2 ] [8 - 7.2] ) give n + ( n − 1 ) + ( n − 2 ) + ⋯ + 8 = 1 2 n ( n + 1 ) − 28 ; n + (n-1) + (n-2) + \cdots + 8 = \tfrac12n(n+1) - 28; the next few terms give ( − 7 ) + ( − 6 ) + ⋯ + ( − 1 ) = − 28 ; (-7) + (-6) + \cdots + (-1) = -28; the last terms are ∑ k = 1 n k = 1 2 n ( n + 1 ) . \sum_{k=1}^n k = \tfrac12n(n+1). The total, then, is ( 1 2 n ( n + 1 ) − 28 ) + ( − 28 ) + 1 2 n ( n + 1 ) = n ( n + 1 ) − 56. (\tfrac12n(n+1) - 28) + (-28) + \tfrac12n(n+1) = n(n+1) - 56. I suspect that you forgot to add in one of the − 28 -28 terms when adding?

Arjen Vreugdenhil - 9 months, 1 week ago

Log in to reply

Ah yes, silly mistake. I see why now. Thanks!

Saúl Huerta - 9 months, 1 week ago
Atomsky Jahid
Aug 31, 2020

For x ≥ n x \geq n ,

g n ( x ) = ∑ k = − n n ∣ x + k ∣ = ∑ k = − n n ( x + k ) = ∑ k = − n n x + ∑ k = − n n k = ( 2 n + 1 ) x \begin{aligned} g_n(x) &= \sum_{k=-n}^{n} |x+k| \\ &= \sum_{k=-n}^{n} (x+k) \\ &= \sum_{k=-n}^{n} x + \sum_{k=-n}^{n} k \\ &= (2n+1) x \end{aligned}

Similarly, for x ≤ − n x \leq -n , g n ( x ) = − ( 2 n + 1 ) x g_n(x) = -(2n+1)x

But, the case we're most interested in is − n < x < n -n < x < n . From the definition of the floor function, ⌊ x ⌋ ≤ x < ⌊ x ⌋ + 1 \lfloor x \rfloor \leq x < \lfloor x \rfloor + 1 . For legibility and ease, we'll use j = ⌊ x ⌋ j = \lfloor x \rfloor throughout the solution.

g n ( x ) = ∑ k = − n n ∣ x + k ∣ = ∑ k = − n − j − 1 ∣ x + k ∣ + ∑ k = − j n ∣ x + k ∣ = − ∑ k = − n − j − 1 ( x + k ) + ∑ k = − j n ( x + k ) = − ∑ k = − n − j − 1 x − ∑ k = − n − j − 1 k + ∑ k = − j n x + ∑ k = − j n k = − ( n − j ) x − j ( j + 1 ) 2 + n ( n + 1 ) 2 + ( n + j + 1 ) x − j ( j + 1 ) 2 + n ( n + 1 ) 2 = ( 2 j + 1 ) x − j ( j + 1 ) + n ( n + 1 ) \begin{aligned} g_n(x) &= \sum_{k=-n}^{n} |x+k| \\ &= \sum_{k=-n}^{-j-1} |x+k| + \sum_{k=-j}^{n} |x+k| \\ &= - \sum_{k=-n}^{-j-1} (x+k) + \sum_{k=-j}^{n} (x+k) \\ &= - \sum_{k=-n}^{-j-1} x - \sum_{k=-n}^{-j-1} k + \sum_{k=-j}^{n} x + \sum_{k=-j}^{n} k \\ &= - (n-j)x - \frac{j(j+1)}{2} + \frac{n(n+1)}{2} + (n+j+1)x - \frac{j(j+1)}{2} + \frac{n(n+1)}{2} \\ &= (2j+1)x - j(j+1) + n(n+1) \end{aligned}

So, f ( x ) = lim ⁡ n → ∞ ( g n ( x ) − n ( n + 1 ) ) = lim ⁡ n → ∞ ( ( 2 j + 1 ) x − j ( j + 1 ) + n ( n + 1 ) − n ( n + 1 ) ) = lim ⁡ n → ∞ ( ( 2 j + 1 ) x − j ( j + 1 ) ) = ( 2 j + 1 ) x − j ( j + 1 ) ⟹ f ( x ) = ( 2 ⌊ x ⌋ + 1 ) x − ⌊ x ⌋ ( ⌊ x ⌋ + 1 ) \begin{aligned} f(x) &= \lim_{n \to \infty} ( g_n(x) - n(n+1) ) \\ &= \lim_{n \to \infty} ( (2j+1)x - j(j+1) + n(n+1) - n(n+1) ) \\ &= \lim_{n \to \infty} ( (2j+1)x - j(j+1) ) \\ &= (2j+1)x - j(j+1) \\ \implies f(x) &= (2\lfloor x \rfloor + 1)x - \lfloor x \rfloor (\lfloor x \rfloor + 1) \end{aligned}

It's interesting to note that f ( x ) f(x) and x 2 x^2 touch when x x is an integer.

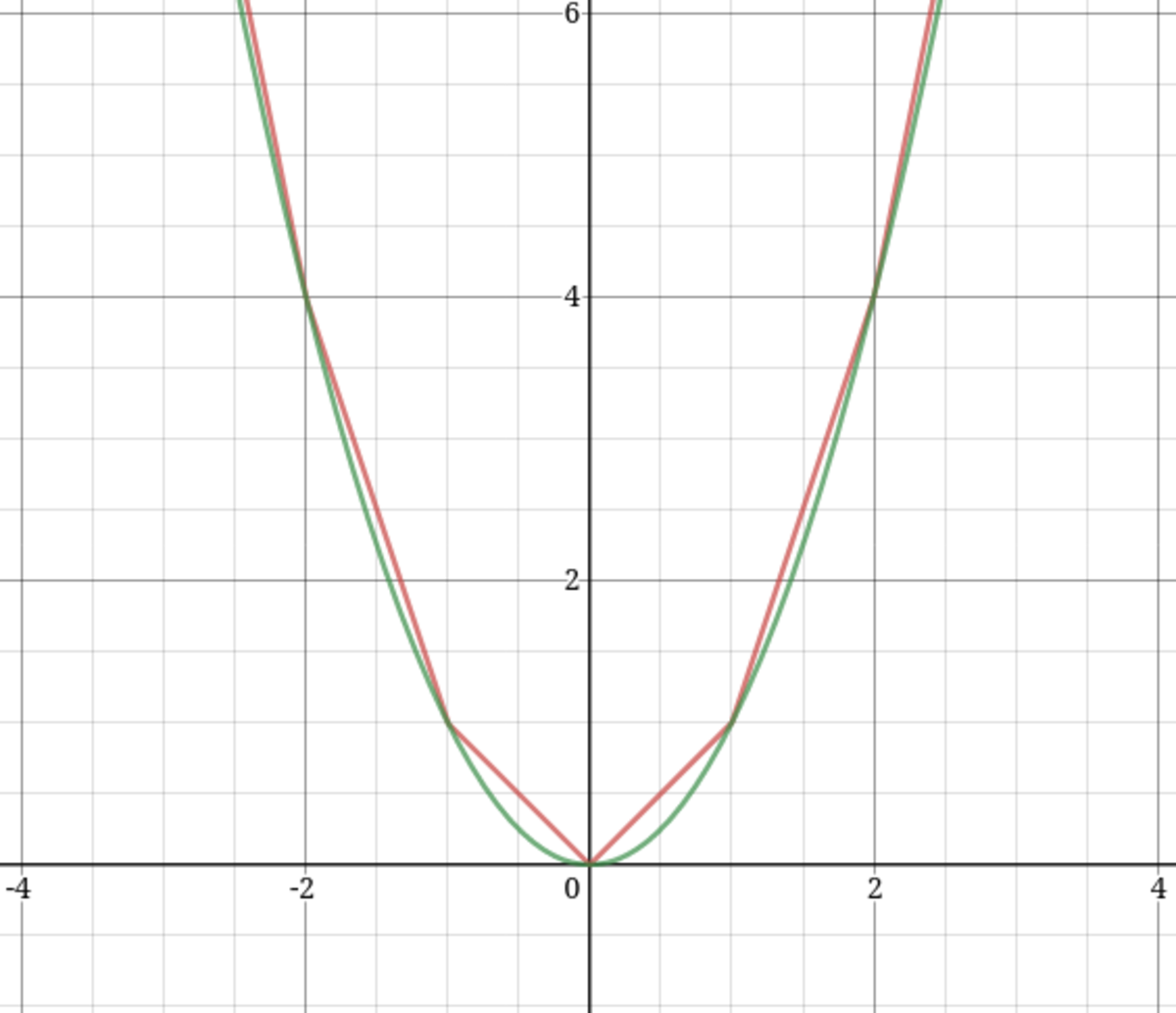Fig: f(x) in red and x^2 in green Fig: f(x) in red and x^2 in green

Lastly, f ( 7.2 ) = ( 2 × 7 + 1 ) 7.2 − 7 ( 7 + 1 ) = 52 f(7.2) = (2 \times 7 + 1)7.2 - 7(7+1) = \boxed{52}

1 Helpful 0 Interesting 1 Brilliant 0 Confused

By writing x = ⌊ x ⌋ + { x } x = \lfloor x \rfloor + \{x\} (so that 0 ≤ { x } < 1 0 \leq \{x\} < 1 is the fractional part of x x ), you can further simplify to f ( x ) = ( 2 ⌊ x ⌋ + 1 ) ( ⌊ x ⌋ + { x } ) − ⌊ x ⌋ ( ⌊ x ⌋ + 1 ) = ⌊ x ⌋ 2 + ( 2 ⌊ x ⌋ + 1 ) { x } , f(x) = (2\lfloor x \rfloor + 1)(\lfloor x\rfloor + \{x\}) - \lfloor x \rfloor (\lfloor x \rfloor + 1) = \lfloor x \rfloor^2 + (2\lfloor x \rfloor + 1)\{x\}, which describes the linear extrapolation, especially if you consider that 2 ⌊ x ⌋ + 1 = ⌊ x + 1 ⌋ 2 − ⌊ x ⌋ 2 2\lfloor x \rfloor + 1 = \lfloor x + 1 \rfloor^2 - \lfloor x \rfloor^2 .

Arjen Vreugdenhil - 9 months, 2 weeks ago

Log in to reply

Yes. If we use floor, ceiling, and fractional functions, we can also write it as f ( x ) = ⌊ x ⌋ 2 + ( ⌈ x ⌉ 2 − ⌊ x ⌋ 2 ) { x } f(x) = \lfloor x \rfloor ^2 + ( \lceil x \rceil ^2 - \lfloor x \rfloor ^2) \{x\}

Atomsky Jahid - 9 months, 2 weeks ago

Log in to reply

That is pretty.

Arjen Vreugdenhil - 9 months, 2 weeks ago

Or, more symmetrically f ( x ) = ⌊ x ⌋ 2 ( ⌈ x ⌉ − x ) + ⌈ x ⌉ 2 ( x − ⌊ x ⌋ ) . f(x) = \lfloor x\rfloor^2(\lceil x \rceil - x) + \lceil x\rceil^2(x - \lfloor x \rfloor).

Arjen Vreugdenhil - 9 months, 2 weeks ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...