AC Current Measurement

We know that $\frac {R}{Z}=cos\theta=cos45=\frac {1}{\sqrt{2}}$ . So $Z=R\sqrt{2}$ .

$\frac {V}{Z}=I$ , so $Z=\frac {V}{I}=\sqrt{2}=R\sqrt{2}$ . So $R=1$ .

Now we know that on phasor diagram, $X_{l}$ and $R$ are perpendicular to each other and the angle between them is

$45$ degrees, which means $X_{l}=R$ or $wL=R=1$ or $L=\frac {1}{w}=\frac {1}{(2\pi f)}=\frac{1}{120\pi}$ .

For next case we have $w=2\pi f=240 \pi$ . So $wL=2$ .

$I=\frac {V}{Z}, Z=\sqrt {R^2+(wL)^2}=\sqrt {1+4}=\sqrt{5}$ .

Thus $I=\frac {1}{\sqrt {5}}=\boxed {0.447}$

Let the source voltage to have a phase angle of 0 and the impedance of the load be $Z=R+\omega Li$ , where $\omega = 2\pi (60)$ is the angular velocity of the alternating current.

Then, the current through the load:

$\begin{aligned} I & = \frac 1{\sqrt 2}\angle -45^\circ \\ \frac VZ & = \frac 1{\sqrt 2}\angle -45^\circ \\ 1\angle 0^\circ & = \frac {Z \angle -45^\circ}{\sqrt 2} \\ \implies Z & = \sqrt 2 \angle 45^\circ \\ R + \omega L i & = 1 + i \end{aligned}$

When frequency is raised from 60 Hz to 120 Hz, we have $Z_1 = R+2\omega L i = 1+2i$ , and:

$\begin{aligned} I_1 & = \frac V{Z_1} = \frac 1{1+2i} = \frac {1-2i}5 \\ \implies |I_1| & = \left| \frac {1-2i}5 \right| = \frac {\sqrt 5}5 \approx \boxed{0.447} \end{aligned}$

Consider the following phasor diagram:

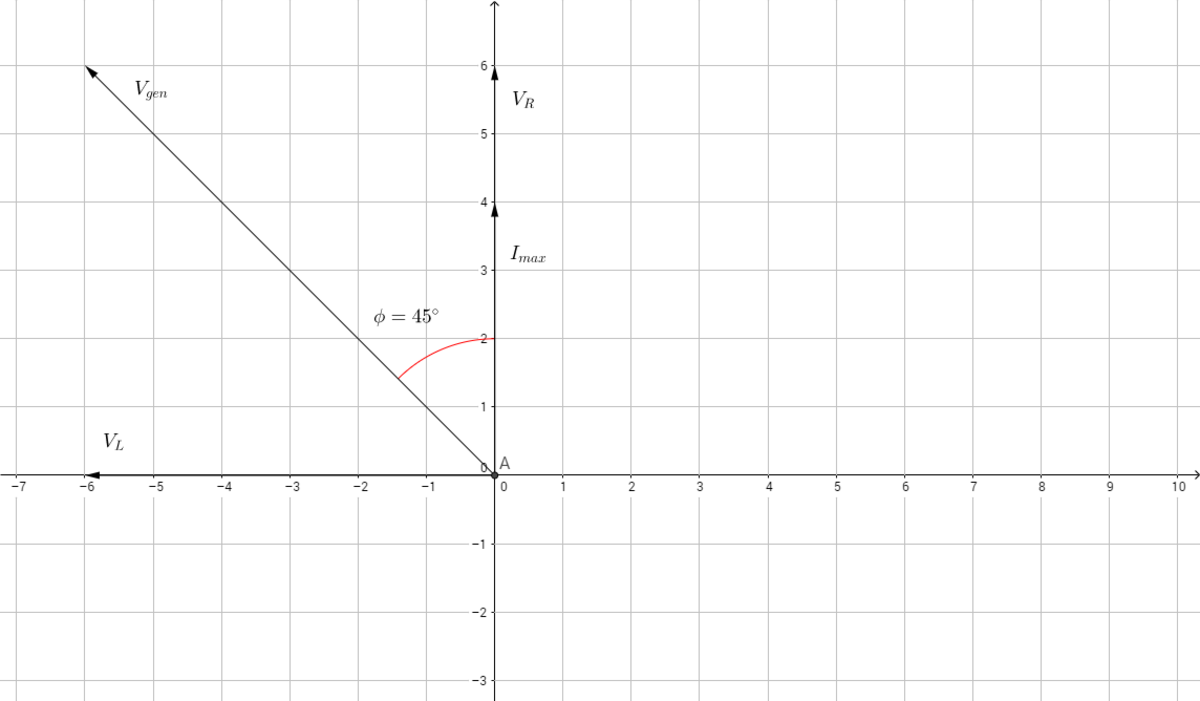
The vectors rotate about the origin counter-clockwise with angular frequency $\omega$ and each has magnitudes corresponding to the maximum voltage/current flowing through the load, with $V_{gen}$ being the maximum generator voltage and $I_{max}$ being the maximum current flowing through the resistor.

The instantaneous magnitudes across each of these elements is given by its corresponding vector's projection on the y-axis, with the sign showing the direction. Note that for an AC circuit $\sqrt{2}M_{rms}=M_{max}$ , where $M$ is the magnitude of the voltage/current across a circuit element.

The impedance of the circuit $Z=\sqrt{R^{2}+X_{L}^{2}}$ , where $X_{L}=\omega L$ , gives us $I_{max}$ , since $V_{gen}=ZI_{max}$

We can also see that $\phi=\tan^{-1} \left( \frac{X_{L}}{R} \right) = 45^{\circ}$ , so we can conclude that in our first scenario $\omega L=X_{L}=R$ . It follows that $V_{rms}=\sqrt{X_{L}^{2}+X_{L}^{2}}I_{rms}$ , and so $X_{L}=R=1\Omega$ .

In the second scenario, the frequency, and as a result the angular frequency, is doubled, so $X_{L}$ is doubled as well. Based on the new conditions, $X_{L}=2\Omega$ and $R=1\Omega$ since the resistor never changed. This makes impedance $\sqrt{5}\Omega$ , and so $I_{rms}=\frac{1}{\sqrt{5}}=\boxed{.447}$