AC Fault Location
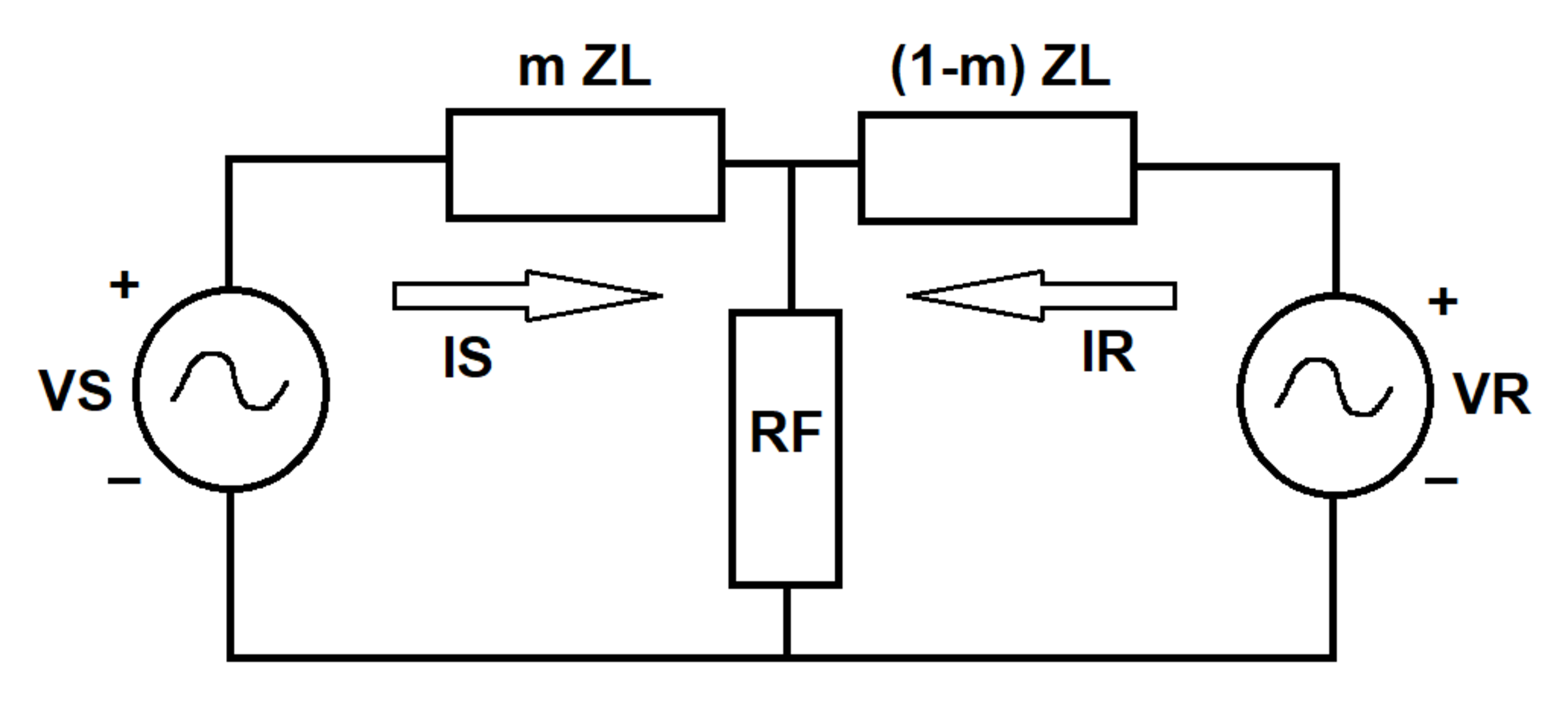
Two single-phase AC voltage sources supply a faulted transmission line. The fault resistance R F divides the line into two impedances: m Z L on the left, and ( 1 − m ) Z L on the right, where 0 < m < 1 . Source voltages V S and V R are known, as well as source currents I S and I R . Real-valued quantities m and R F are unknown.
Determine the value of m .
Details and Assumptions:
1)
V
S
=
9
+
j
5
2)
V
R
=
1
0
+
j
0
3)
Z
L
=
0
+
j
1
0
4)
I
S
=
1
.
4
6
6
4
7
4
2
4
2
9
5
+
j
0
.
0
5
5
2
7
4
7
5
6
6
1
5
8
5)
I
R
=
0
.
0
6
7
6
1
1
8
5
6
9
6
7
8
−
j
0
.
1
2
6
2
6
7
2
0
6
4
3
2
6)
j
=
−
1
The answer is 0.37.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
A fault is an unintended short circuit
To make this one easy to understand, I will write out the equations, which can then be put into matrix form. The first equates two expression for the voltage at the fault point. The second makes a loop from the left side through the fault resistance.
V S − m Z L I S = V R − ( 1 − m ) Z L I R V S − m Z L I S − R F ( I S + I R ) = 0
Solve these two equations for m and R F
@Steven Chase
can we track someone's location using phone number .
If yes ,how to do it?
If no,how police and military officers can do that ,I have seen in films.
Thanks in advance.
Applying Kirchhoff's laws for this circuit leads to the equations cast into a matrix form as such:
[ Z L I S − Z L I R I S + I R I S + I R ] [ m R F ] = [ V S V R − I R Z L ] ⟹ m = [ 1 0 ] [ Z L I S − Z L I R I S + I R I S + I R ] − 1 [ V S V R − I R Z L ] = 0 . 3 7 ⟹ R F = [ 0 1 ] [ Z L I S − Z L I R I S + I R I S + I R ] − 1 [ V S V R − I R Z L ] = 6
From a mathematical point of view, this circuit is easy to solve, but I do not quite grasp the intuition behind a 'fault'. Some explanation of that would be helpful.