AC Load Voltage
In the AC circuit below, there are voltage sources and complex impedances. What is the magnitude of the voltage V , shown in red?
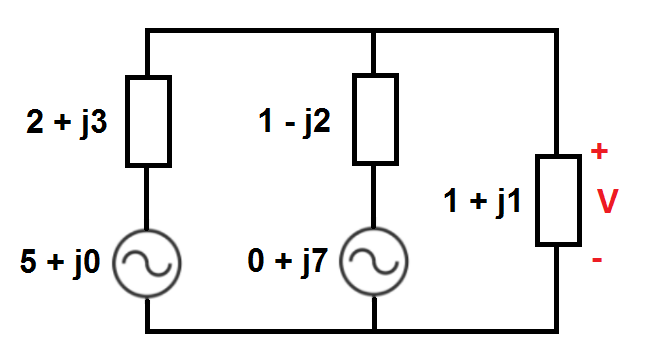
The answer is 2.234.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice solution. Out of curiosity, why do you prefer superposition over nodal analysis?
Log in to reply
Actually, I remember superposition better. Thanks for your solution, I will use node and loop analysis the next round.
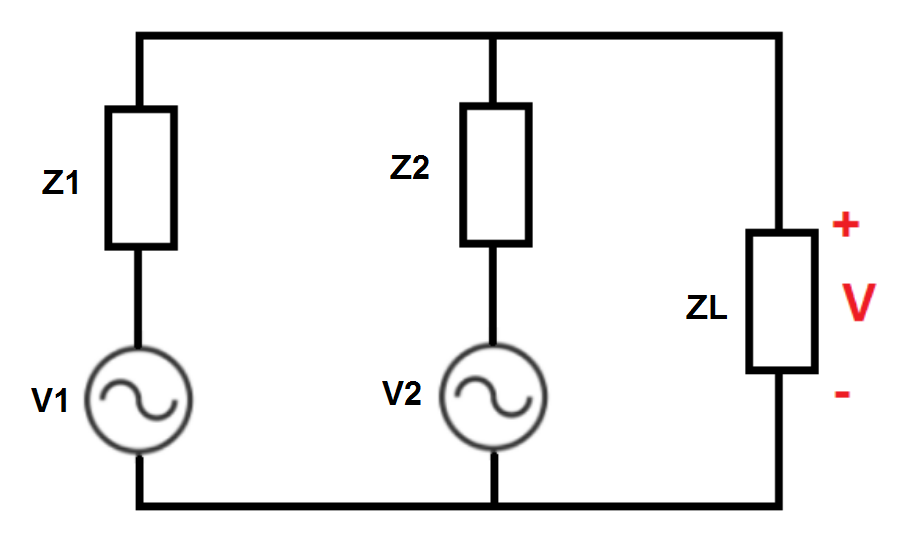
The current flowing out of the top node is zero
Z 1 V − V 1 + Z 2 V − V 2 + Z L V − 0 = 0 V ( Z 1 1 + Z 2 1 + Z L 1 ) = Z 1 V 1 + Z 2 V 2 V = Z 1 1 + Z 2 1 + Z L 1 Z 1 V 1 + Z 2 V 2
By principle of superposition, the given circuit is equivalent to the addition of two circuits on the right as shown above, such that:
V = V 1 + V 2 = 2 + j 3 + ( 1 − j 2 ) ∣ ∣ ( 1 + j ) ( 1 − j 2 ) ∣ ∣ ( 1 + j ) ( 5 + j 0 ) + 1 − j 2 + ( 2 + j 3 ) ∣ ∣ ( 1 + j ) ( 2 + j 3 ) ∣ ∣ ( 1 + j ) ( 0 + j 7 ) = 3 . 4 + j 3 . 2 1 . 4 + j 0 . 2 ( 5 + j 0 ) + 1 . 6 8 − j 1 . 2 4 0 . 6 8 + j 0 . 7 6 ( 0 + j 7 ) = 1 . 2 3 8 5 3 2 1 1 − j 0 . 8 7 1 5 5 9 6 3 3 + − 3 . 4 0 3 6 6 9 7 2 5 + j 0 . 3 2 1 1 0 0 9 1 7 = − 2 . 1 6 5 1 3 7 6 1 5 − j 0 . 5 5 0 4 5 8 7 1 6 ≈ 2 . 2 3 4 ∠ 1 4 . 2 6 5 ∘