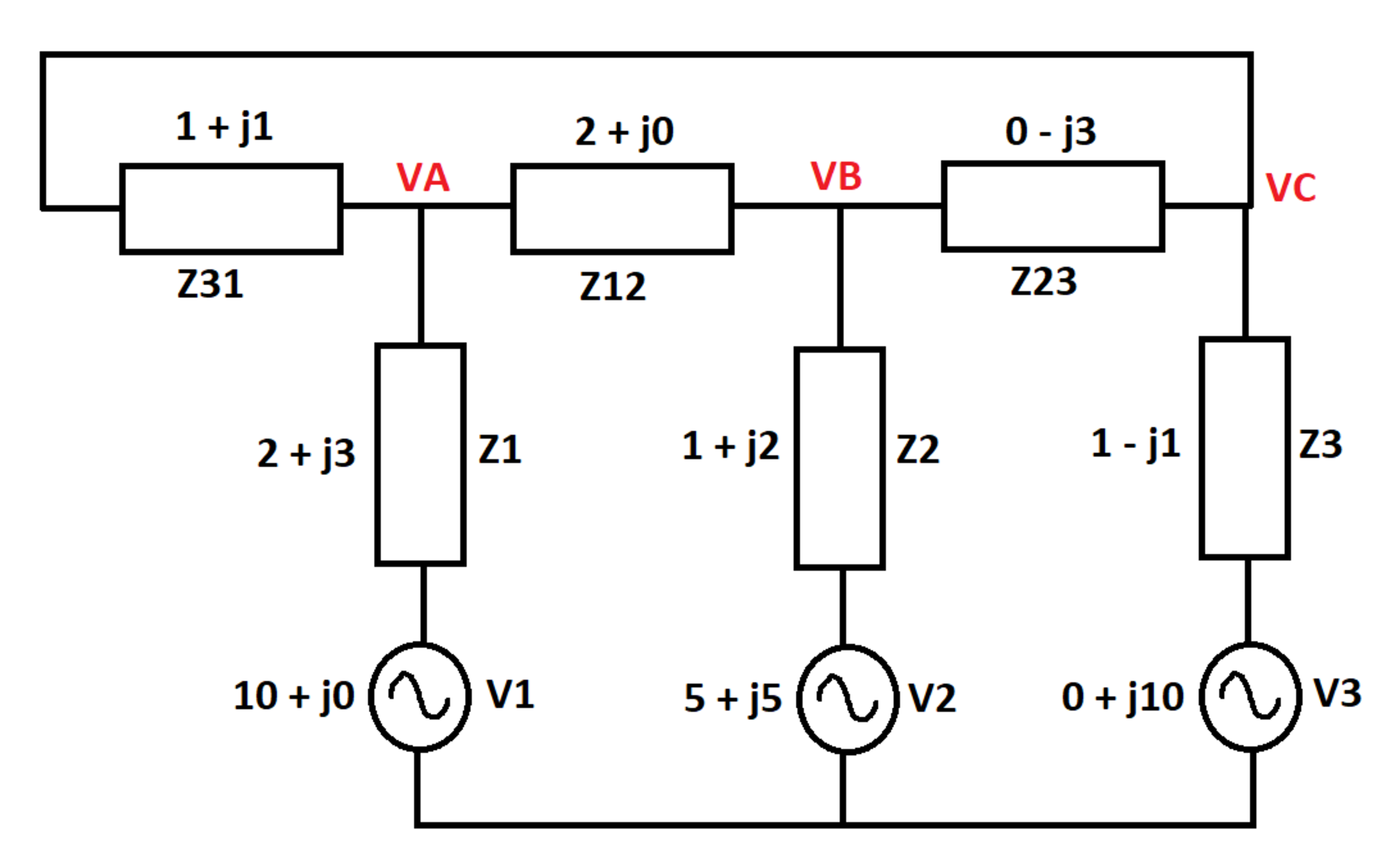
AC Network

I will include a few supplementary notes. Assume that we have solved for the currents as @Karan Chatrath has shown. I used the following two ways to calculate the total active power:

Method 1:
$P = |I_{1}|^2 \, Re(Z_1) + |I_{2}|^2 \, Re(Z_2) + |I_{3}|^2 \, Re(Z_3) + |I_{12}|^2 \, Re(Z_{12}) + |I_{23}|^2 \, Re(Z_{23}) + |I_{31}|^2 \, Re(Z_{31})$

Method 2:

Assume that source currents $(I_1, I_2, I_3)$ are leaving the sources:

$P = Re(V_1 \, I_1^*) + Re(V_2 \, I_2^*) + Re(V_3 \, I_3^*)$

In the above equation, the "*" symbol denotes the complex conjugate, and "Re" denotes the real part of a complex number. We could also have used similar $V I^*$ expressions for each of the six impedances.

The circuit equations are:

$-V_1 + I_1Z_1 - I_4Z_{12}-I_2Z_2 +V_2 = 0$ $-V_2 + I_2Z_2 + I_5Z_{23} - I_3Z_3 +V_3 = 0$ $(I_1+I_4)Z_{31} - I_5Z_{23}+I_4Z_{12} = 0$ $I_2 = I_2 + I_5$ $I_4 +I_1 +I_5 + I_3 = 0$

Solving gives the branch currents. The voltages:

$V_A = V_1 - I_1Z_1$ $V_B = V_2 - I_2Z_2$ $V_C = V_3 - I_3Z_3$

The total power for all impedances is:

$P_{total} = (V_1 - V_A)I_1 + (V_2 - V_B)I_2 + (V_3 - V_C)I_3 + (V_A - V_C)(I_1 + I_4) + (V_B - V_A)I_4 + (V_B - V_C)I_5$

This evaluates to:

$P_{total} = -\frac{152}{17} - j\frac{514}{17}$

Now, as per my limited understanding of AC circuits, the active power is the real part of the above complex number. However, the answer is the imaginary part $\boxed{\frac{514}{17} = 30.2353}$ . I always thought that the imaginary part is reactive power and not active power. My question is that why is the complex part of the total power the active power and not vice versa?