AC Power 10-25-2020

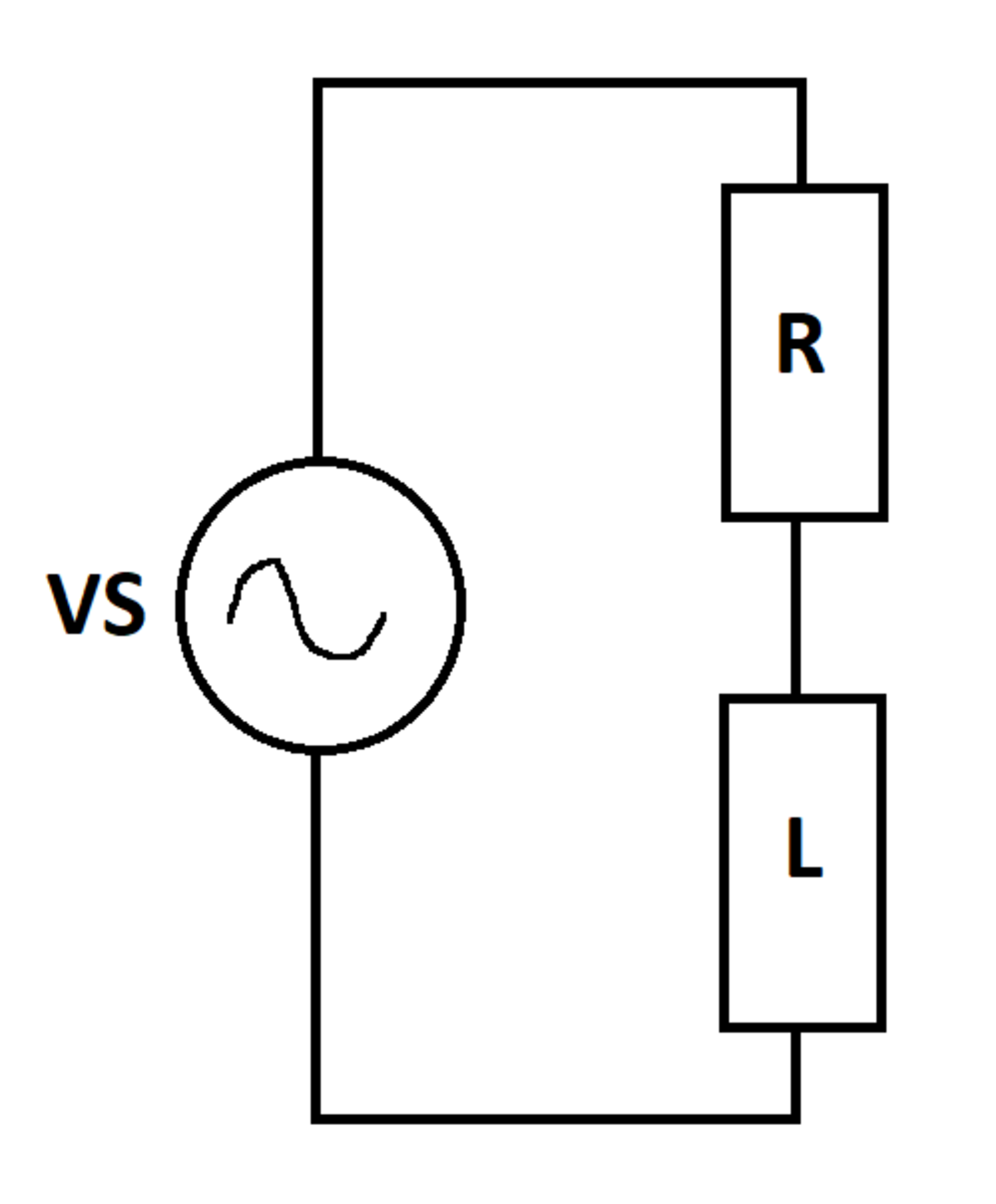
Electricity and Magnetism Level pending

An AC voltage source supplies an RL load. In AC steady-state, what is the average power (in Watts) dissipated by the resistor?

Note: This problem does not require the solution of differential equations

Details and Assumptions:
1) $V_S(t) = 10 \sqrt{2} \sin(2 t )$
2) $R = L = 1$

1 solution

Steven Chase
Oct 26, 2020

The rms source voltage is $10$ , and we can arbitrarily assign it a phase angle of zero. The circuit impedance is:

$Z = R + j \omega L = 1 + j 2$

The current is:

$I = \frac{10}{1 + j2}$

The magnitude of the current is:

$|I| = \frac{10}{\sqrt{1^2 + 2^2}} = \frac{10}{\sqrt{5}}$

The resistor power is:

$P_R = |I|^2 R = \frac{100}{5} 1 = 20$