AC Power Accounting (1-17-2021)

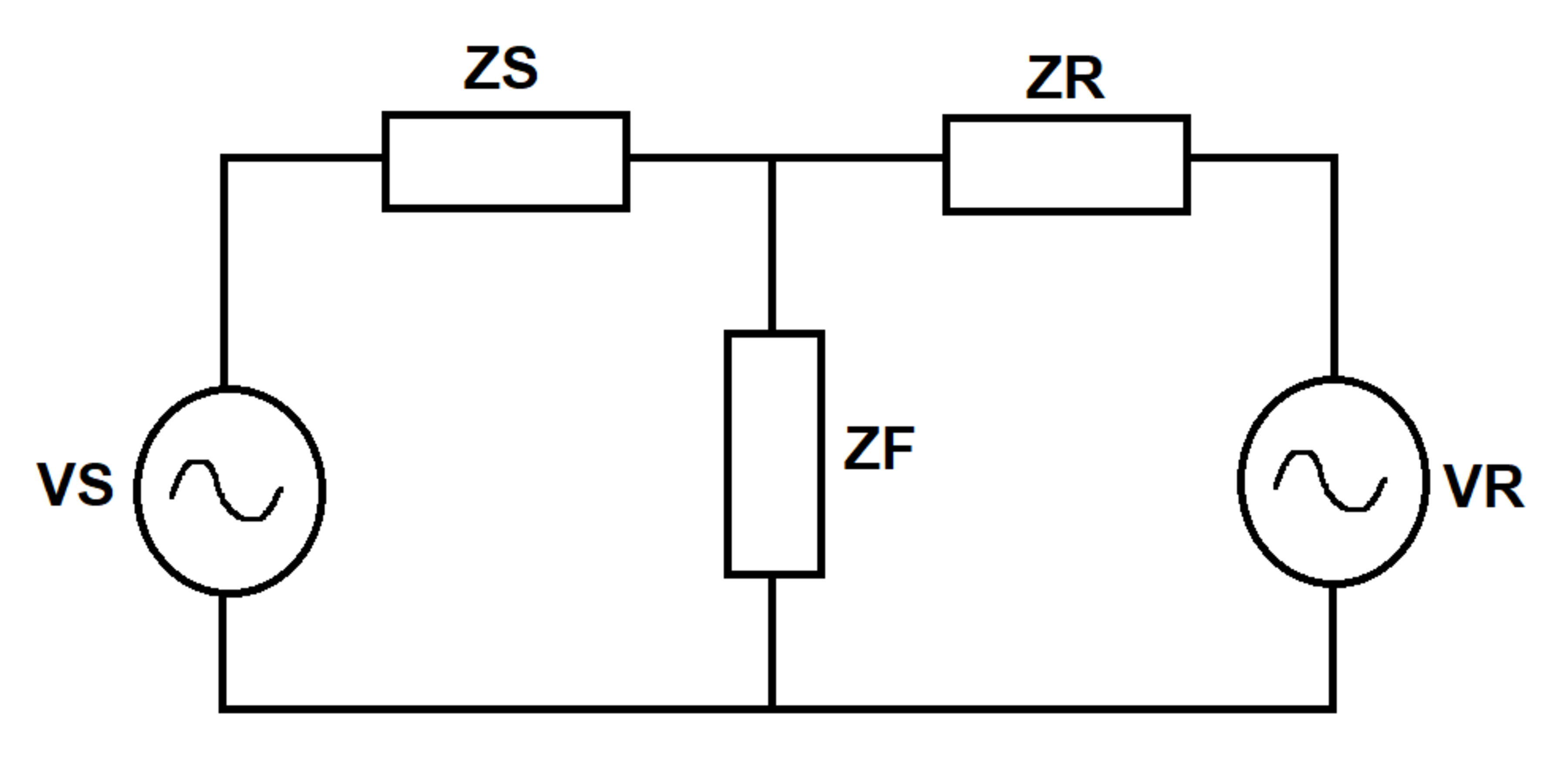
Electricity and Magnetism Level pending

Two AC voltage sources excite a circuit with three impedances as shown in the diagram. Source V S V_S supplies what fraction of the active power consumed by Z F Z_F ?

Details and Assumptions:
1) j = − 1 j = \sqrt{-1}
2) V S = 0 + j 10 V_S = 0 + j 10
3) V R = 10 + j 0 V_R = 10 + j 0
4) Z S = Z R = 0 + j 5 Z_S = Z_R = 0 + j 5
5) Z F = 1 + j 0 Z_F = 1 + j 0


The answer is 0.7.

Steven Chase by Steven Chase , 37, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Karan Chatrath
Jan 17, 2021

Circuit equations in matrix form:

[ Z S + Z F Z F Z F Z R + Z F ] [ I S I R ] = [ V S V R ] ⟹ A I = b \left[\begin{matrix} Z_S+Z_F&Z_F\\Z_F&Z_R+Z_F\end{matrix}\right]\left[\begin{matrix} I_S\\I_R\end{matrix}\right]= \left[\begin{matrix} V_S\\V_R\end{matrix}\right]\implies AI = b ⟹ I = A − 1 b \implies I = A^{-1}b I F = I S + I R = [ 1 1 ] I I_F = I_S+I_R = \left[\begin{matrix} 1&1\end{matrix}\right]I I S = [ 1 0 ] I I_S = \left[\begin{matrix} 1&0\end{matrix}\right]I I R = [ 0 1 ] I I_R = \left[\begin{matrix} 0&1\end{matrix}\right]I

The matrix notation eases the number crunching while using the calculation tool of my choice. Active power supplied by V S V_S :

P S = r e a l ( V S I S ∗ ) P_S = \mathrm{real} \left(V_S I_S^{*}\right) Active power consumed by Z F Z_F :

P F = r e a l ( ( I F Z F ) I F ∗ ) P_F = \mathrm{real} \left((I_FZ_F) I_F^{*}\right)

P S P F = 0.7 \boxed{\frac{P_S}{P_F} = 0.7}

The ' ∗ * ' superscript denotes complex conjugate.

2 Helpful 2 Interesting 2 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...