AC Power Accounting
Let be the combined power (in watts) consumed by all of the resistors in the circuit. Let be the power (in watts) supplied by ideal voltage source to the rest of the circuit.
What is ?
Details:
1)
Voltage magnitudes
. All voltage source phase angles equal
Hint: If the voltage of the source is and the current flowing out of the source is , the active power flowing out of the source is , where the " " symbol denotes the complex conjugate of the current. If we calculate the powers flowing out of all sources and add them up, how does the sum compare to the total power consumed by the resistors?
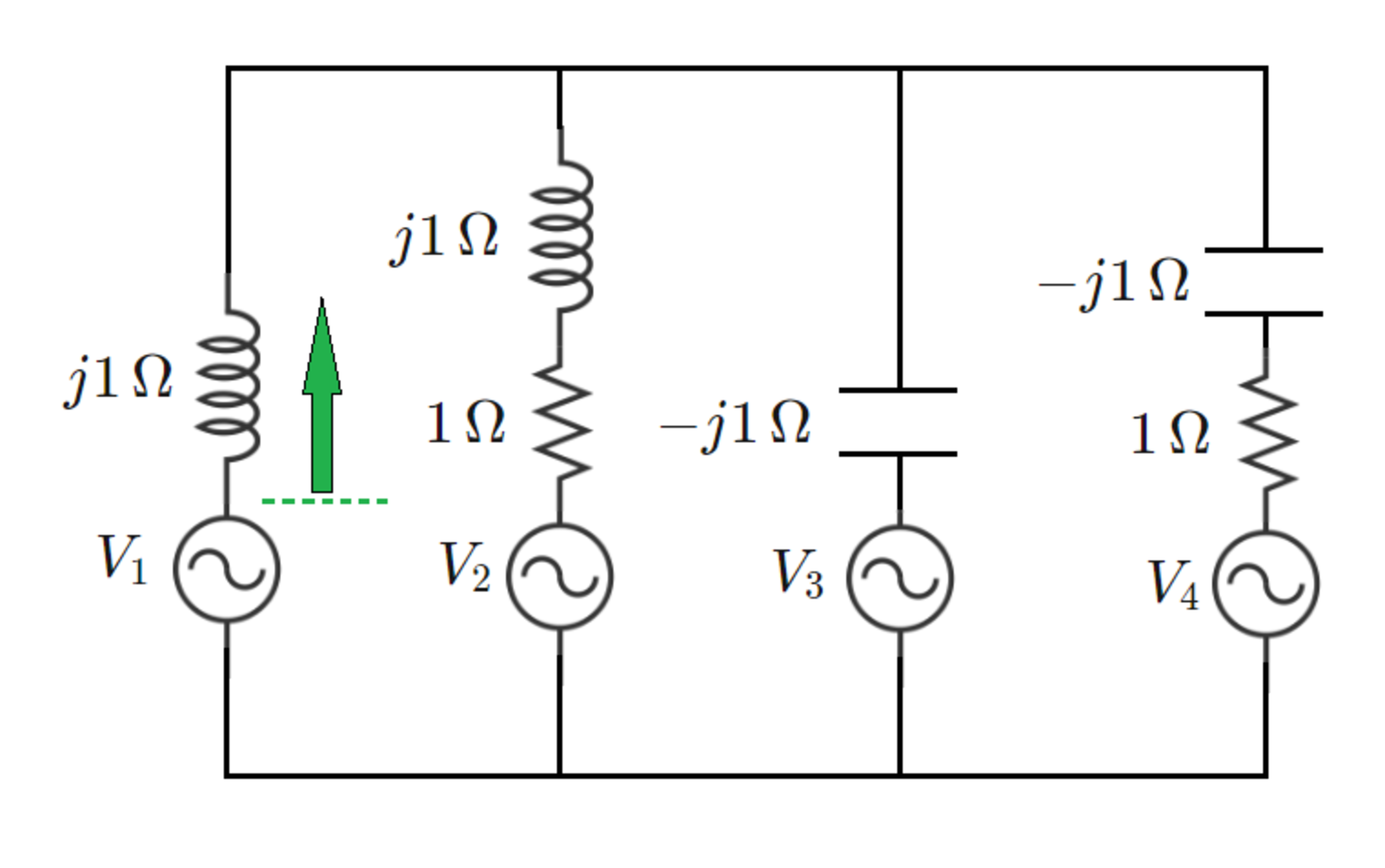
The answer is 1.1538.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
0 solutions
No explanations have been posted yet. Check back later!