Acceleration in a swing
A little boy swings back and forth on the playground. At the highest point in his swing his speed is zero, and at his lowest point his speed is greatest.
Where in the trajectory will his acceleration be zero?
Caution: The acceleration is the rate of change of velocity and not the rate of change of speed .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
but isn't this problem like a pendulum, where the acceleration is zero at the lowest point ,or is that the problem is asking net acceleration (radial + tangential component).
Log in to reply
The swing behaves exactly like a pendulum. In a pendulum / swing, acceleration is not zero at the lowest point because it has non-zero radial acceleration.
The question hasn't specified anything about radial or tangential components of the acceleration, so we must proceed considering the net acceleration.
Log in to reply
For further clarification, I have added a note that says "acceleration is the rate of change of velocity (net acceleration) and not the rate of change of speed (tangential acceleration)."
I'm puzzled by something.
Let's imagine that at the point where the boy reaches the bottom of his swing, the point he's suspended from starts moving at the same velocity (and direction) that he is at that point, so that he switches from moving in a circle to moving in a straight line (horizontal to the earth). After this change, his velocity is constant, and his acceleration is zero. Does the boy's acceleration go instantaneously from non-zero to zero at this point?
(It might be easier to imagine this in reverse: start with the boy and the point of suspension moving together, and then the point of suspension stops moving and the swing switches to circular motion; in this case it would seem that the acceleration would have to go instantaneously from zero to non-zero.)
Log in to reply
Yes, you are right. If you stop/start the top most point instantly then the bottom most point will also gain a sudden acceleration. You may also say that there will be a sudden change in the tension of the thread.
This is a very nice question. Yes, there is indeed a discontinuity in the acceleration of the boy. Just before the change, the boy's acceleration was non-zero and towards the center of the circle. Just after the change, the acceleration is zero.
Something very close to this situation actually happens in real life. If the rope joining the swing to the point of suspension breaks (and it most likely to break at the lowermost point), then the swing stops moving in a circle and starts moving in a parabola. The acceleration changes from towards the center of the circle to downwards (because of gravity) in a very short period of time. We can explain this change in acceleration by seeing that when the rope breaks, the net force on the boy changes so the acceleration changes.
It should be noted that in real life there can't be discontinuities in the acceleration of an object. Even though the breaking of rope appears instantaneous, it takes place over a small instant of time (I think a few milliseconds). The acceleration changes very rapidly in this instant, so the boy would experience a large, but finite jerk when the rope breaks.
As he swings downward in either direction, he experiences positive acceleration due to gravity. As he swings upward he experiences negative acceleration or deceleration due to gravity. At some point, his acceleration goes from positive to negative and back again - passing through zero acceleration in the process. So non-zero throughout cannot be correct.
Log in to reply
No, it is meaningless to say that the direction is positive or negative as the direction is changing continuously. If the motion occurs in a straight line then your argument would have been correct as there would be only two possible directions of the acceleration.
Here is a video clip that shows how the acceleration varies with the position.
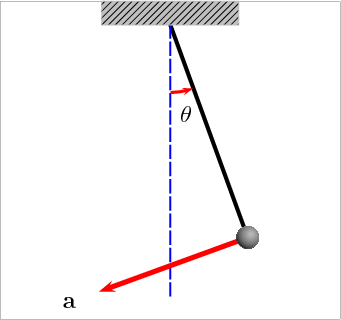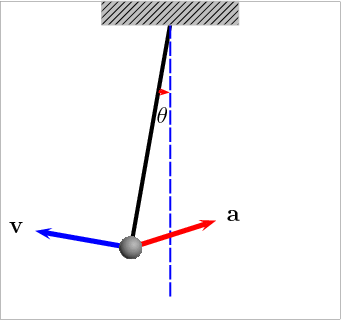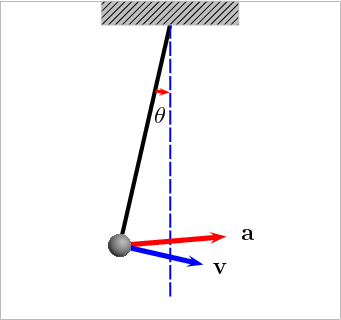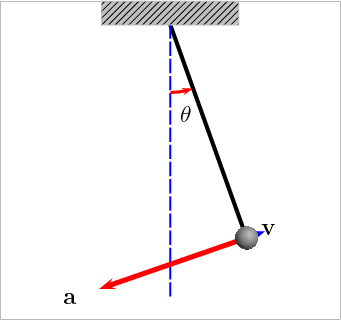
Log in to reply
Thanks - this is a huge help. It shows the resultant vector that combines acceleration due to gravity, which is always downward, and rotational acceleration.
Oh I see why the answer is that now. Was really confused because so used to taking the velocity as the magnitude. Thanks a bunch for the graph, its quite interesting that that is the case and how the velocity when taken as a planar vector changes
The problem statement is somewhat confusing. There are two points where it is stated that v=0 and one point where it is stated that v=max. If we are to take velocity to be a vector in the plane then it does not make sense to say that v reaches a maximum, because there is not a natural ordering of the vectors in the plane. It makes sense to say that the magnitude of v reaches a maximum at the bottom of the arc. But magnitude of velocity is speed, and it is noted that acceleration is the rate of change of velocity, not speed. So in one reference the problem is asking us to consider v to act like a (positive) scalar variable and then we are told to treat v like a planar vector.
It is a little confusing to even say that v=0 at the top of the swing. Normally we consider 0 to be a number. But if v is a vector then it takes the value of the zero vector at the top of the swing. It is common to not differentiate between the number zero and the zero vector, so many times we write 0 for both instead of having a special notation for the zero vector.
The acceleration is zero at the lowest point because in that point the resultant of forces and the sum of their moment is zero, so zero forces zero acceleration
At the lowest point, he experiences a radial / centripetal acceleration (because of circular motion) but no tangential acceleration because his speed is not changing at that instant (it is at a maximum). At the extreme point, he experiences no radial acceleration (because his speed is zero), but he does experience a tangential acceleration because the radial swing chain tension is not perfectly co-linear with the gravity force.
He experiences a radial centripetal force, but this is opposed by the reaction in the chain. Hence no radial acceleration. The lengths of the chains are constant, so if you differentiate this twice to give acceleration, you'll get zero radial acceleration. Also, the tangential (circumferential) acceleration is zero because the velocity is a sinusoid and there are times when the derivative of this are zero. So, the answer, I believe, is wrong.
Log in to reply
The radial acceleration does not change the radius, rather it rotates the direction of the velocity. Moreover, the centripetal force is not a force that acts on a particle in circular motion, rather whatever force that acts on the particle towards the center is called the centripetal force.
In this case, at the bottom most point two forces are acting on the swing. First, the tension in the chain ( T ) and second is the gravitational force ( m g ). The net force towards the center is T − m g and this is called the centripetal force. It is wrong to state that the centripetal force balances this force and hence the net force/acceleration is zero.
If the acceleration were equal to zero, that would mean that the velocity of the swing would be constant. One may think that the acceleration is equal to zero on both the highest point, because the velocity at both points are the same. However, you must also keep in mind that the velocity change from the top point to the low point definitely causes a change in velocity, and vise-versa. Therefore, the velocity of the swing is constantly changing, so no point in the system does the swing have an acceleration of zero.
Velocity need not be constant if the acceleration of the boy is zero only at a particular instant. Like, imagine a case where the velocity varies as v = t − t 2 then acceleration will be a = 1 − 2 t . This implies the acceleration is zero at a particular instant t = 0 . 5 s , although the velocity is continuously varying.
Log in to reply
I knew that, I probably didn't explain my thoughts very well in my solution!
Whilst I know what you are getting at, I would contest that the Heisenberg uncertainty principle applies :). At any given moment of measuring velocity, the acceleration has to be zero because the velocity is unchanging when you measure it.
Log in to reply
Well, that is why we have calculus. We take an infinitesimally small interval for the measurement of acceleration at a moment.
this swing accelerates forward and backward. for it to change direction it must have an acceleration equal to zero at some point otherwise it will continue in one direction forever.
Log in to reply
This argument would be correct for 1D motion or in this case for tangential acceleration only. The tangential component of acceleration is zero at the bottom most point.

Log in to reply
I'm puzzled by these easily mistaken terms speed and velocity. I'm German and in school and university, I had only the one term "Geschwindigkeit" (speed) for the scalar version, and "speed vector" for the vectorial version. The same with acceleration: "acceleration" for the scalar value, and otherwise "acceleration vector". Symbolic distinction also is easy, because we write vectors always with arrow above, scalars without.
So for me the answer "at lowest point" was a logical consequence, because—in my thinking—otherwise I'd have expected the question: "Where in the trajectory will his acceleration vector be zero?" (with correct answer: It is non-zero throughout).
Lesson learned. With English text I'll have to watch much more closely whether it's a scalar value or a vector.
I agree with the solution, but if you consider a dt when the velocity is máx, so the acceletration's vector will be turnning your way...
Acceleration due to gravity will be constant throughout the boy's motion (-9.81 ms − 2 ).
The following are the points of misconception for this problem,
V = 0 does not necessarily imply a = 0 : It is generally thought that if the speed is zero then the acceleration is also zero . This is not necessarily true. Consider a case where a ball is thrown vertically upwards. At the highest point, the speed equals zero whereas the acceleration equals to the acceleration due to gravity. Similarly, in this problem, at the extreme positions, although the speed is zero, the acceleration is not zero. The acceleration is zero where the net force is zero. But, at the extreme positions, the tension and the gravity are not along the same line, hence, they cannot cancel each other.
At the lowest point, the tension is opposite to the gravity and it appears as if they are canceling each other, but they don’t. A particle moving in a circular motion must have a net acceleration towards the center. This is called the centripetal acceleration and is equal to R v 2 . Here, v is the speed of the particle and R is the radius of its circular path.
If we consider any small section of the motion, we will find that either the speed is changing or the direction of velocity is changing. Therefore, there will be no instance when the acceleration is zero.