Acceleration of hinges
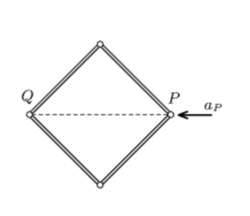 Four similar rods of uniform density are connected with frictionless hinges. This frame is placed on a horizontal smooth tabletop, such that its shape is a square. Vertex P is acted upon by a horizontal force in the direction of the diagonal, and due to this force it begins to move at an acceleration of
.
Four similar rods of uniform density are connected with frictionless hinges. This frame is placed on a horizontal smooth tabletop, such that its shape is a square. Vertex P is acted upon by a horizontal force in the direction of the diagonal, and due to this force it begins to move at an acceleration of
.
If the initial acceleration of the opposite vertex Q is then find k.
k is positive if Q moves away from P and k is negative if Q moves closer to P
The answer is -0.2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The problem can be solved with the work-energy theorem.
If we call the mass of the entire system M , then the applied force will be 0 . 5 M ( a P + a Q ) because 0 . 5 ( a P + a Q ) is the acceleration of the center of mass. After a time dt, hinge P moves a distance 0 . 5 a P ( d t ) 2 therefore the work done will be:
Work = 0 . 2 5 M a P ( a P + a Q ) ( d t ) 2
Now we find the energy of the system after a time dt. I did this in two separate ways. The first way was to use coordinates x p , the position of hinge p, and D the distance between hinge P and hinge Q. The other way was to use coordinates x p and θ , the angle of the rods with the horizontal. Both ways worked. The derivation of the energies is not hard, but I will not show it. If you do it you will find:
Rotational Kinetic Energy = 4 8 M ( a Q − a P ) 2 ( d t ) 2
Vertical Kinetic Energy = 3 2 M ( a Q − a P ) 2 ( d t ) 2
Horizontal KE = 4 M ( ( 0 . 2 5 a Q + 0 . 7 5 a P ) 2 + ( 0 . 7 5 a Q + 0 . 2 5 a P ) 2 ) ( d t ) 2
The horizontal kinetic energy has two terms because the left and right side move at different speeds, whereas the rotational and vertical kinetic energy of each rod is the same by symmetry, so there is only one term for those.
If you set the sum of these three energy terms equal to the work, you will arrive at the solution a Q = 5 − 1 a P
(The other solution to the quadratic equation is a Q = a P but this will not happen because the hinges are frictionless.)