Acceleration with pulley
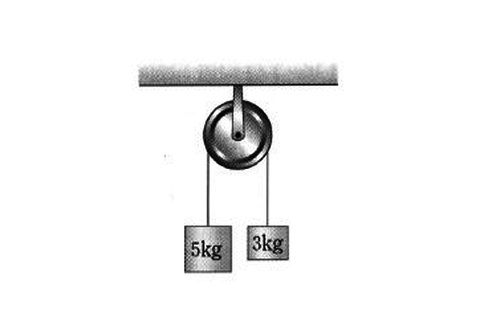 In the above diagram, two objects with their respective masses
kg and
kg are hung on a pulley with no friction. Find the magnitude of acceleration
of the left object with mass
kg.
In the above diagram, two objects with their respective masses
kg and
kg are hung on a pulley with no friction. Find the magnitude of acceleration
of the left object with mass
kg.
Gravitational acceleration is m/s .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let m1=5 kg, m2=3kg
We know that in this pulley system Fnet=FT(tension force)+ FG(force of gravity), but since there is only one pulley it means that both masses are experiencing the same FT(supporting force FN or in this case FT) and we can reduce the FT so that we are left with Fnet=FG.
FG1= m1*g
FG2= m2*g
Now we know that if one of the block is moving down, it means that the other must be moving, therefore let's make FG1 be in positive direction and FG2 be in negative direction.
Fnet= sum of all forces Fnet=FG1 + (-FG2)
Fnet= m*a
49N + (-29.4N) = (m1+m2) * a
19.6N = 8a
19.6/8 = 8a/8 , this reduces the 8 from 8a, so we divide both sides by 8
a=2.45 m/s^2
Since we used 9.8 m/s^2 for g, we get a=2.45 m/s^2 but if we used g=10 m/s^2, like it does in the question, a should equal to 2.5 m/s^2.
This is my first answering to anything, so please forgive me for any unconventional methods! Hope this solution was well explained and useful! Thanks!