ACDC (Part 2)
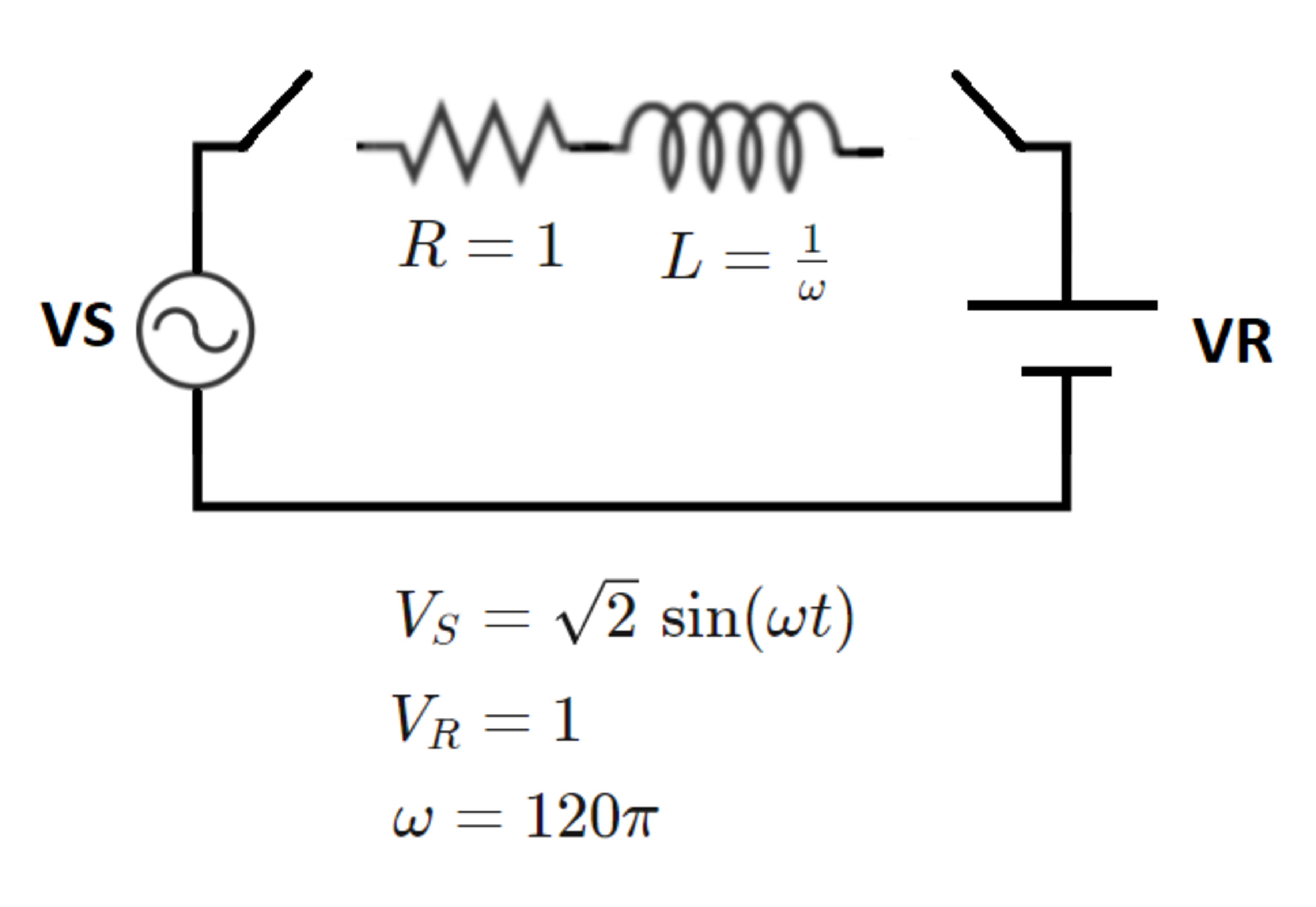
In the circuit below, the switches close at time , and the inductor is initially de-energized.
When the time-derivative of the current is zero for the first time, what is the instantaneous magnitude of the current?
Note: Give your answer as a positive number
The answer is 0.248.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Differential equation of the circuit is: v S ( t ) − R i − L d t d i − V R = 0 This is a first-order linear non-homogeneous DE. We have two "inputs" to the equation, one is a constant - V R - and the other is sinusoidal - v S . Since the equation is linear, we can solve separately for each input and then superpose solutions to get the solution to our two-input equation. These inputs are very common, so I will just write out the final solution without derivation: i ( t ) = hom. part C e − L R t + const. input − R V R + sinusoidal input ∣ Z ∣ V S sin ( ω t − ϕ ) where ∣ Z ∣ = R 2 + ω 2 L 2 and ϕ = arctan R ω L . Constant C is determined from initial condition i ( t = 0 ) = 0 which is implied since any amount of current will produce a magnetic field inside the inductor, contrary to what was said in the question. Once we determine C and plug in given values, we get: i ( t ) d t d i = ( 1 + 2 1 ) e − 1 2 0 π t + sin ( 1 2 0 π t − 4 π ) − 1 = 1 2 0 π [ − ( 1 + 2 1 ) e − 1 2 0 π t + cos ( 1 2 0 π t − 4 π ) ] By numerical means we find that first time that time-derivative of the current is 0 is at t ≈ 0 . 0 0 1 4 8 6 and we find current i ≈ − 0 . 2 4 8 3 7 9 .
I assumed that the starting polarity of AC source is the opposite of the DC source, but this should've been explicitly marked in the question. Also, in writing out DE I assumed the direction of the current to be clockwise.