ACDC

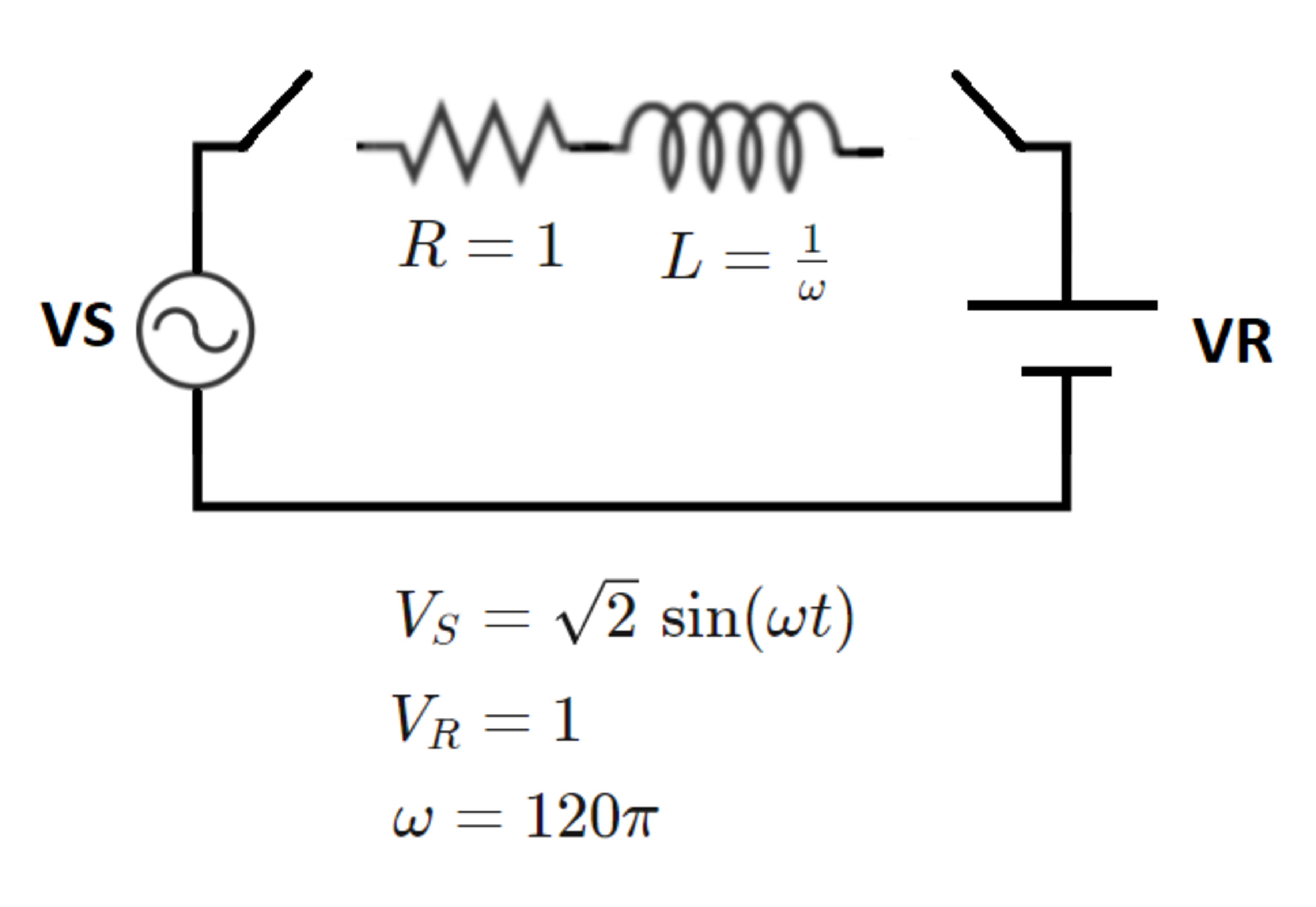
Electricity and Magnetism Level pending

In the circuit below, the switches close at time $t = 0$ , and the inductor is initially de-energized. Let $I_{max}$ be the maximum current magnitude seen for $t > 0.1$ , and let $I_{min}$ be the minimum current magnitude seen for $t > 0.1$ .

What is $I_{max} + I_{min}$ ?

Note: The problem is asking for magnitudes, which are positive numbers.
Hint: Superposition is helpful here. $t > 0.1$ essentially represents steady-state conditions

The answer is 2.0.

1 solution

Karan Chatrath
Oct 12, 2019

The equation of the circuit is:

$\frac{dI}{dt} + I\omega= (V_S - V_R)\omega$

Taking Laplace transform on both sides gives:

$(s+\omega)I_s = \left(\frac{\sqrt{2}\omega}{s^2 + \omega^2} - \frac{1}{s}\right)\omega$

$I_s = \frac{1}{s+\omega}\left(\frac{\sqrt{2}\omega}{s^2 + \omega^2} - \frac{1}{s}\right)\omega$

Taking the inverse Laplace transform to obtain current as a function of time by referring to any standard table of Laplace transforms gives:

$I(t) ={\mathrm{e}}^{-t\,\omega}-\cos\left(\frac{\pi }{4}+t\,\omega\right)+\frac{\sqrt{2}\,{\mathrm{e}}^{-t\,\omega}}{2}-1$

As time progresses, the decaying exponentials tend towards zero, and therefore the steady-state solution is:

$I_{ss}(t) = -\cos\left(\frac{\pi }{4}+t\,\omega\right)-1$

It can be easily concluded from here that the above expression has a maximum value of zero and a minimum value of negative two. The answer is therefore $\boxed{2}$ . I got an initial attempt wrong as I missed the word 'magnitude'.

Nice Laplace solution, thanks. Another way to see it is that by superposition, there is 1 amp of DC current in steady state, as well as 1 amp (peak) of AC current.

Steven Chase - 1 year, 8 months ago

Superposition is a faster route to the answer. Should have approached it this way. I tend to go the diff. eq. route by default.

Karan Chatrath - 1 year, 8 months ago

ACDC

The answer is 2.0.

1 solution

0 pending reports