Acoustic interference
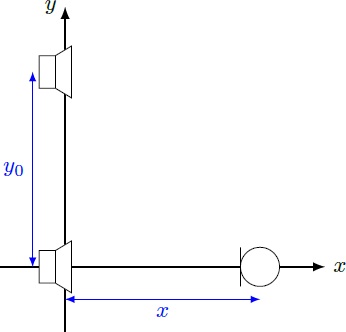
Two loudspeakers located on the y-axis at and produce a sine wave with the same amplitude, phase and frequency . A microphone on the x-axis receives the sound signal from the two speakers. Due to interference between the two sound signals, the volume of the sound received by the microphone oscillates as function of . How many interference minima are observed between and ?
Assumptions: The speakers can be treated as point sources that emit spherical waves. The speed of sound is .
The answer is 17.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The wave length of the sound results λ = c / f = 0 . 4 m . For destructive interference, the paths of the two waves must differ by an odd multiple of half the wavelength 2 ( 2 n + 1 ) λ = r 2 − r 1 = x 2 + y 0 2 − x mit n = 0 , 1 , 2 , … with radial distances r 1 and r 2 between source and receiver. Solving for x results ⇒ ⇒ ⇒ 2 ( 2 n + 1 ) λ + x 4 ( 2 n + 1 ) 2 λ 2 + ( 2 n + 1 ) λ x + x 2 x = x 2 + y 0 2 = x 2 + y 0 2 = ( 2 n + 1 ) λ y 0 2 − 4 2 n + 1 λ For sufficiently large n , the position x becomes negative, so that there is no longer a valid solution. The maximum value of n is given by zeroing x ⇒ ⇒ 0 ( 2 n ∗ + 1 ) 2 n ∗ = ( 2 n ∗ + 1 ) λ y 0 2 − 4 2 n ∗ + 1 λ = λ 2 4 y 0 2 = λ y 0 − 1 = 1 6 . 5 Therefore, valid numbers are in the range n ∈ { 0 , 1 , … , 1 6 } , so that there are 17 interference minima.