Across Squares

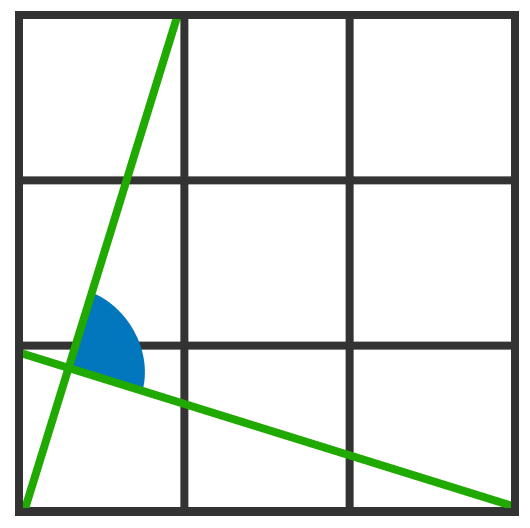
Relevant wiki: Equations of Parallel and Perpendicular Lines

Let the gradient of the green line that touches the corner of the top left square be $m_1$ ,

and let the gradient of the green line that touches the corner of the bottom right square be $m_2$ .

The gradient of a curve can be calculated as "rise over run", that is, the ratio of the difference of the vertical distance, and the horizontal distance, respectively.

So $m_1 = \dfrac31 = 3$ . And $m_2 =\dfrac{-1}{3}$ . Since the product $m_1 m_2$ is equal to -1, then they must be perpendicular to each other. And so, the angle between them is $\boxed{90^\circ}$ .

The two lines are perpendicular, because their slopes are opposite reciprocals.

The two triangles (vertical one 1x3, and horizontal one 3x1) are congruent. And one triangle is rotated by 90 degrees with respect to the other. So angle between corresponding lines must be 90 degrees!

If you tilt the bottom three squares and the line segment they hold about 90° anticlockwise about the center of the leftmost bottom square the two line segments will be equal, which can quite easily be determined geometrically. Therefore the angle in between the line segments must be 90°