Summation Thug Life!

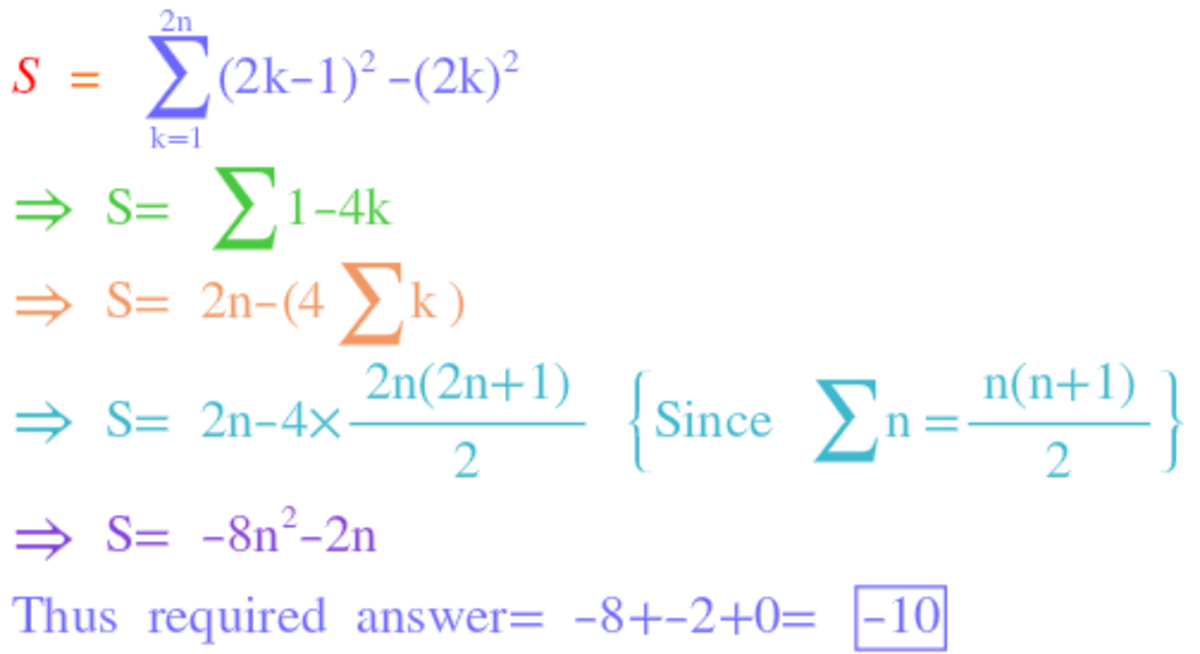
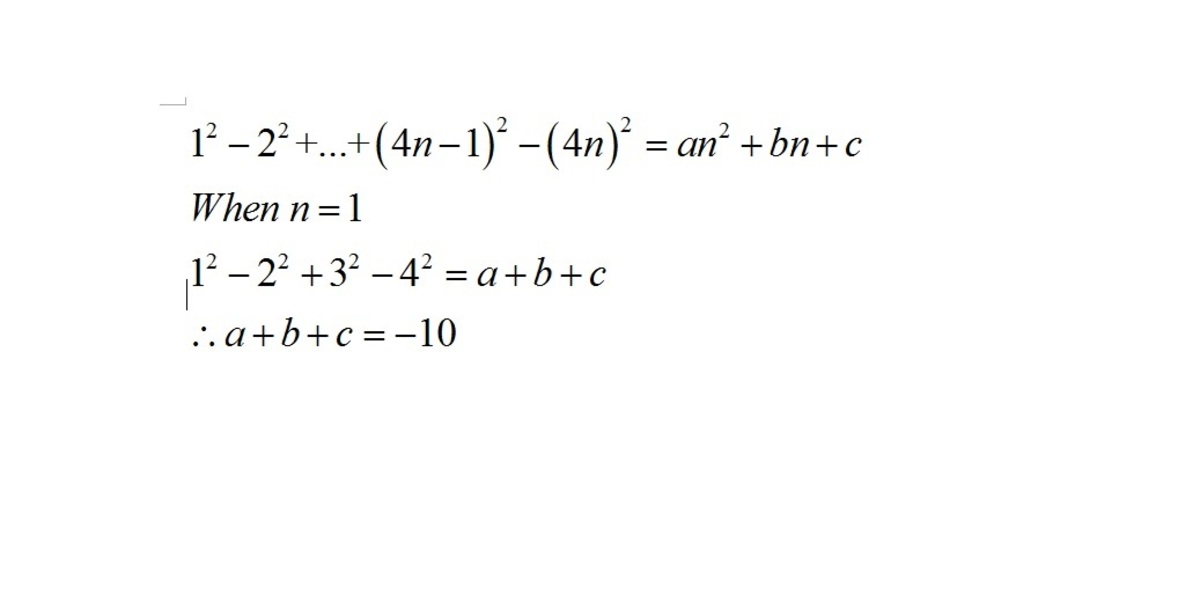
Rearranging the expression into groups like this: $(1^2- 2^2) + (3^2 - 4^2) + (5^2- 6^2) + \cdots = (-3) + (-7) + (-11) + \cdots$

This expression represents an arithmetic progression with first term $a= -3$ , common difference, $d= -4$ . Since we adjusted 2 terms in one group, no. of terms in this AP have to be taken as $\dfrac{4n}2 = 2n$ .

So, using the arithmetic progression sum formula:

$\begin{aligned} S &=& \dfrac N2 \left [2a + (N-1)d \right ] \\ &=& \dfrac{2n}2 \left [ 2(-3) + (2n-1)(-4) \right ] \\ &=& n(-6 - 8n + 4) \\ &=& n(-8n - 2 ) \\ &=& -8n^2 - 2n + 0 \end{aligned}$

Comparing it with $an^2 + bn + c$ shows that $a=-8, b=-2, c=0$ . Thus our answer is $a+b+c=\boxed{-10}$ .

$\begin{matrix} S & = & 1^{ 2 } & - & 2^{ 2 } & + & 3^{ 2 } & - & 4^{ 2 } & + & \dots & + & { \left( 4n-1 \right) }^{ 2 } & - & { \left( 4n \right) }^{ 2 } \\ -S & = & 2^{ 2 } & - & 1^{ 2 } & + & 4^{ 2 } & - & 3^{ 2 } & + & \dots & + & { \left( 4n \right) }^{ 2 } & - & { \left( 4n-1 \right) }^{ 2 } \end{matrix}$

${ n }^{ 2 }-{ \left( n-1 \right) }^{ 2 }=\left( n-n+1 \right) \left( n+n-1 \right) =n+n-1=\left( n-1 \right) +n$

$-S=1+2+3+4+\dots +\left( 4n-1 \right) +4n\\ -S=\frac { 4n\left( 4n+1 \right) }{ 2 } =8{ n }^{ 2 }+2n\\ S=-8{ n }^{ 2 }-2n$

input n=1, then use the formula until n=1 equaling to a+b+c.