Addition Distributes over Multiplication?

$x_1 + x_2 + \ldots + x_U = B$ Recall that if we have $U$ positive integers that sum up to $B$ , we can set up the bijection with placing $B$ balls into $U$ urns. Hence, there are ${ B - 1 \choose U - 1 }$ ways. This is known as the stars and bars approach.

---

$a ( b + c) = ab + ac \Leftrightarrow a ( a+b+c - 1 ) = 0$

Let's consider the following cases:

Case 1. $a = 0$ .
Then $b ,c$ can be any value, so there are $21 \times 21 = 441$ possibilties.

Case 2. $a > 0$ .
We must have $a + b + c = 1$ .
Use the change of variables $x \rightarrow a, y \rightarrow b + 11, z \rightarrow c + 11$ . Then we are looking for positive integer solutions to

$x + y + z = a + (b+11) + (c+11) = 23, 1 \leq x \leq 10, 1 \leq y \leq 21, 1 \leq z \leq 21$

We apply PIE to the restrictions of $x \geq 11, y \geq 22 , z \geq 22$ . We are looking for the number of solutions that satisfy none of these conditions.
If there are no restrictions, then there are ${ 22 \choose 2 } = 231$ .
If we have the single restriction $x \geq 11$ , then using the change of variables $X \rightarrow x - 10$ , we are looking for positive integer solutions to $X + y + z = 13$ , of which there are ${ 12 \choose 2 } = 66$ solutions.
If we have the single restriction that $y \geq 22$ , then using the change of variables $Y \rightarrow y - 21$ , we are looking for positive integer solutions to $x + Y + z = 2$ , of which there are ${ 1 \choose 2 } = 0$ solutions.
Similarly, if we have the single restriction that $z \geq 22$ , then there are ${ 1 \choose 2 } = 0$ solutions.
If we have any pair of restrictions, clearly there are no solutions.
If we have all 3 restrictions, clearly there are no solutions.

Hence, in this case, there are $231 - (66 + 0 + 0 ) + (0+0+0) - 0 = 165$ solutions.

Case 3. $a < 0$ . We must have $a + b + c = 1$ .
Use the change of variables $x \rightarrow - a , y \rightarrow -b + 11, z \rightarrow -c + 11$ . Then, we are looking for positive itneger solutions to

$x + y + z = -a + (-b+11) + (-c+11) = 21 , 1 \leq y \leq 21, 1 \leq z \leq 21$

We apply PIE to the restrictions of $x \geq 11, y \geq 22, z \geq 22$ . We are looking for the number of solutions that satisfy none of these conditions.
If there are no restrictions, then there are ${ 20 \choose 2 } = 190$ .
If we have the single restriction $x \geq 11$ , then using the change of variables $X \rightarrow x - 10$ , we are looking for positive integer solutions to $X + y + z = 11$ , of which there are ${ 10 \choose 2 } = 55$ solutions.
If we have the single restriction that $y \geq 22$ , then using the change of variables $Y \rightarrow y - 21$ , we are looking for positive integer solutions to $x + Y + z = 0$ , of which there are $0$ solutions in positive integers. Similarly, if we have the single restriction that $z \geq 22$ , then there are $0$ solutions in positive integers.
If we have any pair of restrictions, clearly there are no solutions.
If we have all 3 restrictions, clearly there are no solutions.

Hence, in this case, there are $190 - (55 + 0 + 0) + (0+0+0) - 0 = 135$ solutions.

Thus, there are a total of $441 + 165 + 135 = 751$ solutions.

Rearrange the equation we get $a = a(a + b + c)$ . With $a\neq 0$ , the equation becomes $a+b+c=1$ , where $a, b, c \in [-10, 10]$ . Now, we will ignore the fact that $a\neq 0$ and eliminate that case later.

Interesting things happen now, move $c$ to RHS to form $a+b=1-c$ . Then this is the space for all combination $a,b$ within their domain.

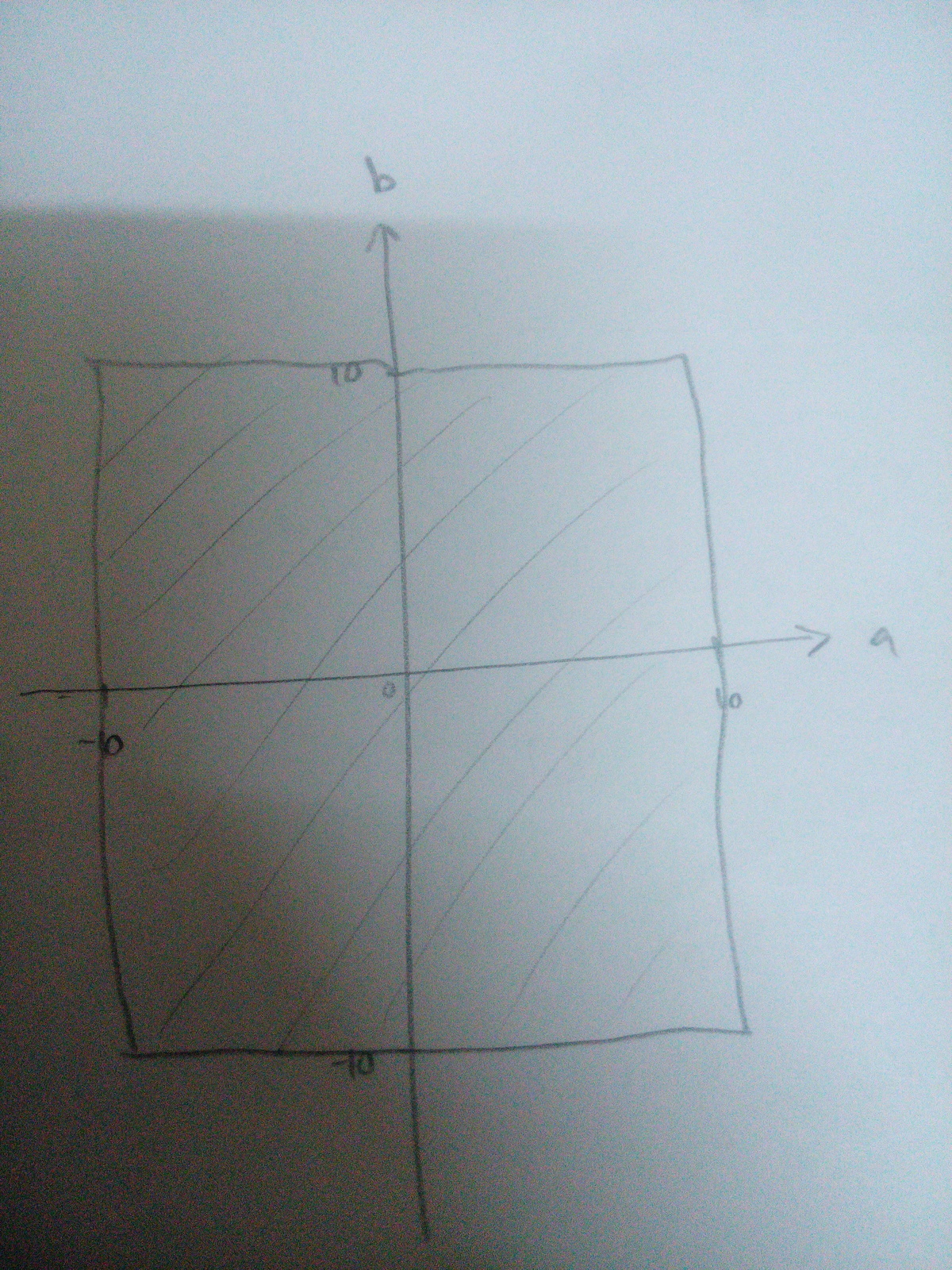
Their sum must be within $1-c \in [-9, 11]$ , which is

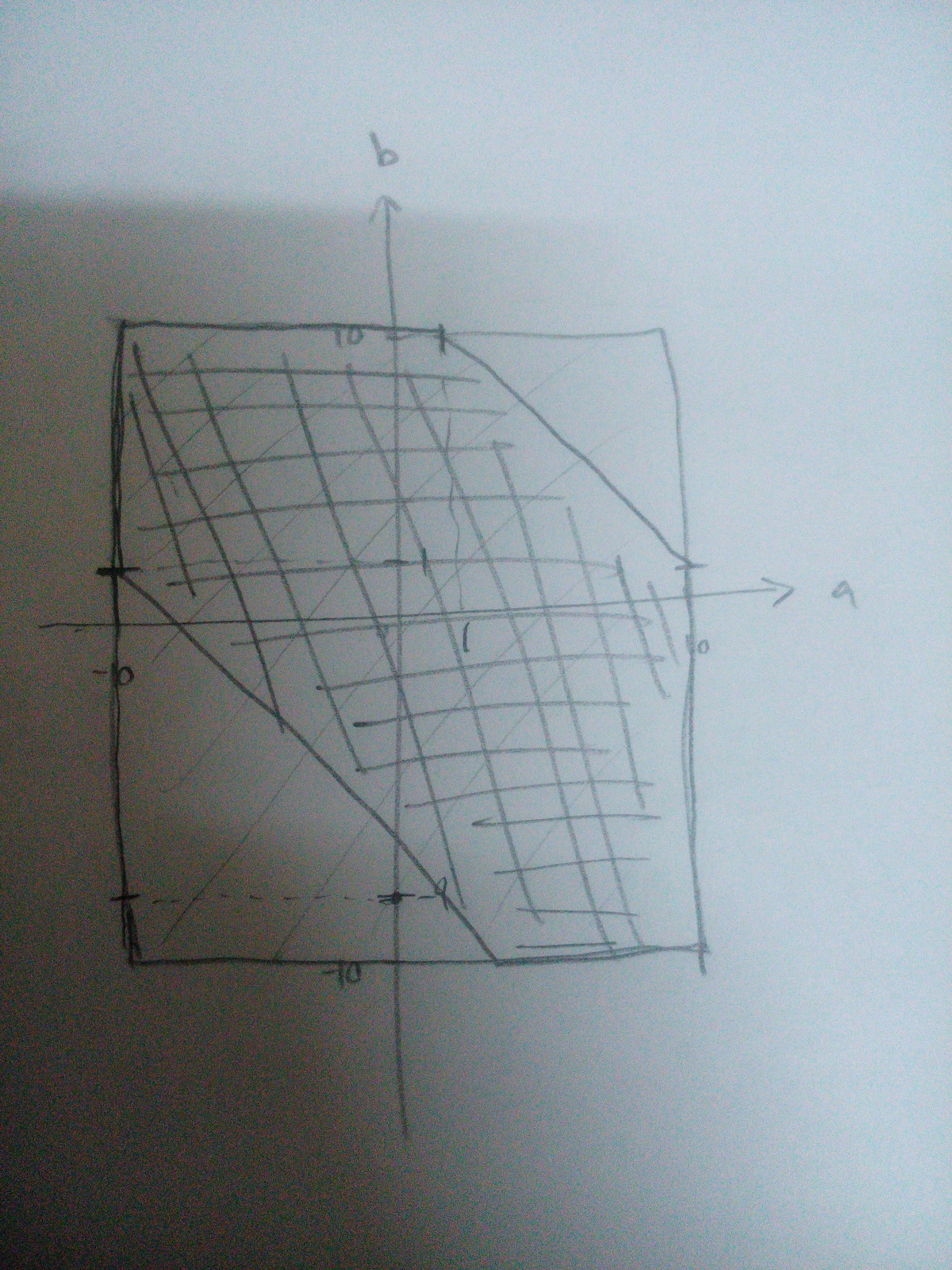
The problem becomes finding the number of lattice points within the polygon. We will do this by applying Pick's Theorem.

$\text{Area} = 20\times 20 - \frac{1}{2} \times 11 \times 11 - \frac{1}{2} \times 9 \times 9$

$\text{B} = 3\times 9 + 3 \times 11$

By Pick's Theorem,

$\text{Area}=I + \frac{B}{2} - 1$

which gives us $I=270$ , so the number of lattice points within the polygon is $I+B=330$ .

Recall that in this case, we considered $a=0$ , but we need not have $b+c=1$ . So we will remove the case $b+c=1$ and add all their combinations. The number of cases where $b+c=1$ is $20$ and their total combinations is $21\times 21=441$ . Hence, the answer is $330-20+441=751$ .

Here's a generating functions solution.

Note that $a + bc = (a+b)(a+c) \iff a = a^2 + a(b+c)$

Case 1: $a = 0$

In this case, $b$ and $c$ can take any value. So, this case gives rise to $21 \times 21 = 441$ solutions.

Case 2: $a \neq 0$

The condition now reduces to $a + b + c = 1$

In this case, the number of solutions is equal to the coefficient of $x$ in the following expression :

$(-1 + A)A^2 \quad \text{where } A = \sum_{r = -10}^{10} x^r = \frac{1}{x^{10}} \frac{1-x^{21}}{1-x}$

where the gp summation formula is used to get the last form of $A$ .

So, the expression now becomes $\frac{1}{x^{30}}\frac{1}{(1-x)^3}(1 - x^{21})^2(1-x^{21} - x^{10}(1-x))\quad (*)$

Now, Newton's binomial theorem shows that $\frac{1}{(1-x)^3} = \sum_{r = 0}^{\infty} \binom {r + 2} 2 x^r$

Simplifying the numerator of (*), we get the following :

$\frac{1}{x^{30}} \left (\sum_{r = 0}^{\infty} \binom {r + 2} 2 x^r \right) (1-x^{10}+x^{11}-3x^{21}+2x^{31}+x^{32}(\text{ some more terms }))$

Hence, the coefficient of $x$ in the expression is ${33 \choose 2} + {22 \choose 2} - {23 \choose 2} - 3{12 \choose 2} + 2{2 \choose 2}= 310$

And so, total number of solutions is $441 + 310 = \boxed{751}$