$a+b+c+d=6.44=a\times b\times c \times d.$

Let $A=100a, B=100b, C=100c$ and $D=100d$ . Then we have $A+B+C+D=644$ and $ABCD=644000000$ .

Since $(u+v)^2-4uv=\left(u-v\right)^2\ge 0$ , we have $(A+B)^2-4AB=(644-C-D)^2-4\times \frac{644000000}{CD} \ge 0$ .

Sketch the graph $y=(644-C-x)^2 -4\times \frac{644000000}{Cx}$ . Using geogebra, we know that $0<y<644$ if $123\le C \l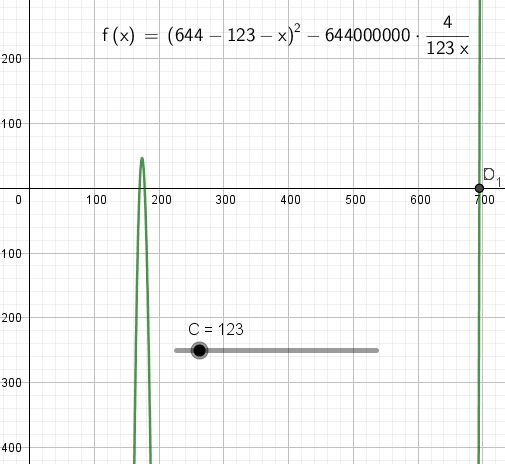e 203$ .

Now consider the factors $w$ of $644000000=7\times 23 \times 2^8 \times 5^6$ , where $123 \le w \le 203$ . We have $w\in \{125, 128, 140, 160, 161, 175, 184, 200\}$ .

Note that, if we choose $C=161=23\times 7$ , then $A,B,D \notin \{140, 175, 184\}$ as each of these numbers has either 7 or 23 as factor. Similarly, we pick exactly one element from $\{140, 175\}$ as both have 7 as factor.

Note that if $C=128=2^7$ , then $A,B,D \notin \{140, 160, 184,200\}$ otherwise $ABCD$ has a factor $2^k$ where $k>8$ . This means that if $C=128=2^7$ , then $A,B,D \in \{125, 161, 175\}$ which is not possible as $161$ and $175$ appear simultaneously. So $128$ is not in the consideration.

Note that if $C=161$ , then $A,B,D \in \{125, 160, 200\}$ which is not possible as $A+B+C+D \neq 644$ . So $161$ is not in the consideration.

So $A,B,C,D \in \{125, 140, 160, 175, 184, 200\}$

Using geogebra again, we know if $C=200$ , $134<x \le162$ , so from the above list, $A,B,D \in \{140, 160\}$ which is not possible. So $200$ is not in the consideration.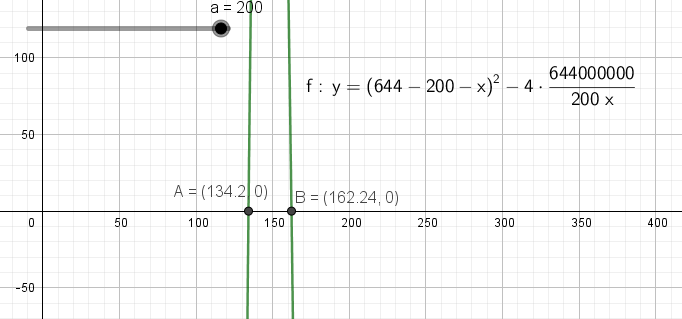

So either $A,B,C,D \in \{125, 160, 175, 184\}$ or $A,B,C,D \in \{125, 140, 160, 184\}$ .

After checking, $A=125, B=160, C=175$ and $D=184$ satisfy the condition.

So $100\left(d-a\right)=D-A=184-125=\boxed{59}$ .