Additive Subtraction
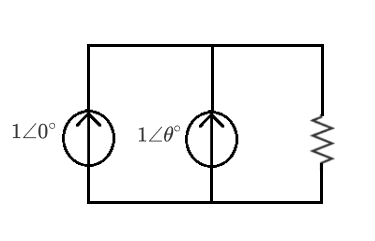
Two ideal AC current sources are connected in parallel to feed a resistive load. The two currents have the same magnitude, and they are out of phase by θ degrees.
If the load current magnitude is 8 0 % as large as that of either source, determine θ . Enter your answer as a positive number in the range ( 0 , 1 8 0 ) , to the nearest whole degree.
The answer is 133.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I suppose the starting angle is irrelevant, so we can use two phasors for the current with e j 2 θ and e − j 2 θ amps. (I picked R = 1 ohm for easy math without loss of generality.)
The currents sum together in the resistor, which gives a total current with magnitude ∣ e j 2 θ + e − j 2 θ ∣ = 2 cos 2 θ .
Setting this to equal to 0.8 amps and solving for θ gives θ = 2 arccos 2 0 . 8 = 1 3 3 o
∣ 1 + e j θ ∣ = 0 . 8
∣ 1 + cos ( θ ) + j sin ( θ ) ∣ = 0 . 8
[ 1 + cos ( θ ) ] 2 + [ sin 2 ( θ ) ] = 0 . 6 4
cos ( θ ) = − 0 . 6 8
θ ≈ 1 3 3 o