Rotation of adiabatic tube
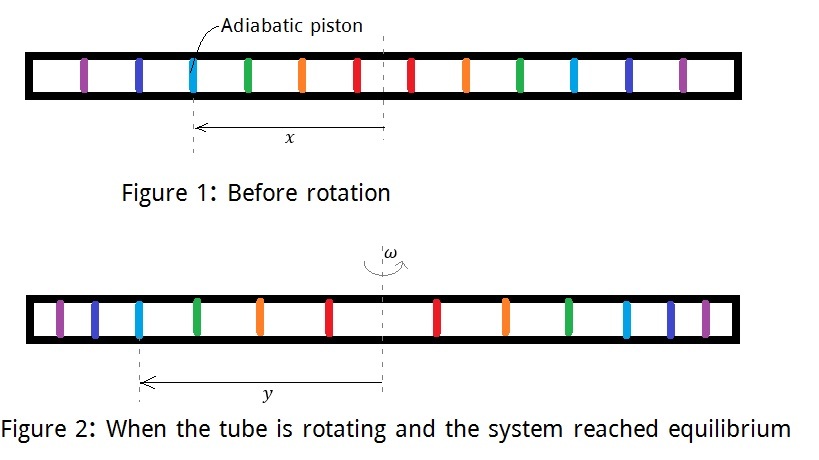
Consider an adiabatic tube which is divided into compartments by movable adiabatic pistons of negligible mass. The compartments have same length. Initially each of the compartments contains gas of same pressure and temperature.
Now, the tube starts to rotate at uniform angular velocity about axis through center perpendicular to length. The length of the compartments are small enough to consider the pressure in a particular compartment constant.
After some period of time, the system comes to equilibrium.
Let, represents the initial position (from the center of the tube) of a piston, and represents its final position.
In the graph , the slope at some point , can be expressed as , where and are constants.
Calculate the absolute value of in unit.
Details and assumptions:
Initial temperature
Angular velocity
Molar gas constant
Molecular mass of the gas and the gas is diatomic.
The answer is 4.15152992.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
As the process is adiabatic [for diatomic gas, heat capacity ratio γ = 5 7 ], p 0 ( Δ x ) γ = p ( Δ y ) γ → Δ x Δ y = ( p p 0 ) γ 1 . . . . . . . . . ( i ) Again, the number of molecules in the compartment is same in both figures. Therefore, ρ ρ 0 = Δ x Δ y Using eqn (i), ρ = ( p 0 p ) γ 1 ⋅ ρ 0 . . . . . . . . . ( i i ) Let the cross-sectional area of the tube is A 0 . So, the net force on the compartment we are talking about is [ p ( y + Δ y ) − p ( y ) ] A 0 . And this is equal to the centripetal force. Therefore, [ p ( y + Δ y ) − p ( y ) ] A 0 = ( ρ A 0 Δ y ) ω 2 y → Δ p = ρ ω 2 y Δ y Using eqn (2), Δ p = ( p 0 p ) γ 1 ⋅ ρ 0 ω 2 y Δ y → p − γ 1 Δ p = ( p 0 γ 1 ρ 0 ω 2 ) y Δ y Let the pressure at the center compartment be p 1 in fig 2. Integrating both sides, ∫ p 1 p p − γ 1 d p = p 0 γ 1 ρ 0 ω 2 ∫ 0 y y d y → − γ 1 + 1 p − γ 1 + 1 − p 1 − γ 1 + 1 = ( 2 p 0 γ 1 ρ 0 ω 2 ) y 2 → ( p 0 p ) − γ 1 + 1 ⋅ p 0 − γ 1 + 1 − p 1 − γ 1 + 1 = ( − γ 1 + 1 ) ( 2 p 0 γ 1 ρ 0 ω 2 ) y 2 Using eqn. 1, ( Δ x Δ y ) − γ ( γ γ − 1 ) ⋅ p 0 γ γ − 1 − p 1 γ γ − 1 = ( 2 γ p 0 γ 1 ( γ − 1 ) ρ 0 ω 2 ) y 2 → d x d y = [ ( 2 γ p 0 ( γ − 1 ) ρ 0 ω 2 ) y 2 + ( p 0 p 1 ) γ γ − 1 ] − γ − 1 1 So we have, A = 2 γ p 0 ( γ − 1 ) ρ 0 ω 2 n = − γ − 1 1 Therefore, n A = − 2 p 0 γ ρ 0 ω 2 Using ideal gas equation, p 0 ρ 0 = R T 0 M Therefore, n A = − 2 R T 0 γ M ω 2