Adjusting the thermometer
Older thermometers are usually made out of a glass tube of mercury with a spherical mercury container at one end. Since mercury is very sensitive to temperature change, a small increase in our body’s temperature causes the mercury in the container to expand and push the mercury in the tube, which we can read off the thermometer. What is the minimal temperature difference in ∘ C our eye can read off in this way?
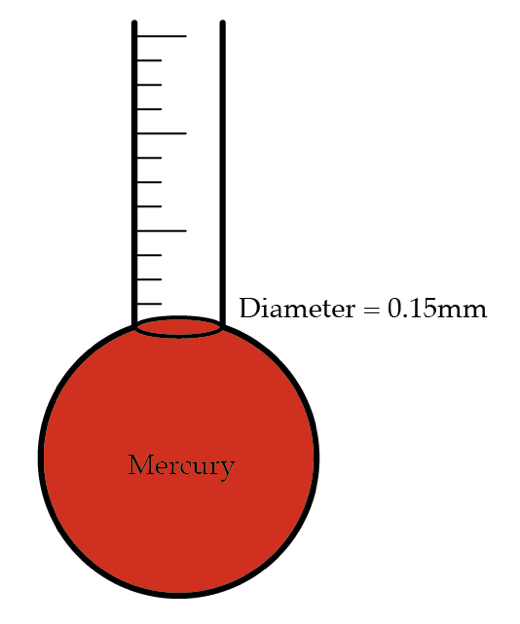
Details and assumptions
- A human eye can distinguish points that are up to 0 . 0 5 mm apart
- Volumetric thermal expansion coefficient of mercury is 0 . 1 8 × 1 0 − 3 K 1
- All expansion happens in the sphere and glass expansion can be neglected
- Ignore gravity effects
- Diameter of thermometer is 0 . 1 5 mm
- Volume of mercury container is 0 . 2 5 5 cm 3
The answer is 0.0193.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
First, find the minimum volume variation that can be seen: [; \mathbf{ \Delta V = cylinder \ area \times minimum \ height} ;], where cylinder area equals [; \mathbf{ 7.5 \times \pi \ mm^2 } ;] and minimum height equals [; \mathbf{ 0.05 \ mm } ;] [; \mathbf{ \Delta V = \pi \times \left (7.5 \times 10^{-2} \right )^2 \times 0.05 = 8.84 \times 10^{-4} mm^3 } ;]
Then, use the volume variation formula: [; \mathbf{ \Delta V = V_{0} \times \gamma \times \Delta \theta } ;] [; \mathbf{ 8.84 \times 10^{-4} = 0.255 \times 10^{3} \times 18 \times 10^(-5) \times \Delta \theta } ;]
Solving for [; \mathbf{ \Delta \theta } ;], we find: [; \mathbf{ \Delta \theta = 0.019 } ;] ° [; \mathbf{ C } ;]
using formula ΔV=V* ɑ d ΔT, we have ΔT= ΔV/(V ɑ), and ΔV=hS=h pi d^2/4. ΔT=h pi d^2/(4V ɑ)=0.05 3.14 0.15 0.15/(4 255 0.18×10^(−3))=0.01924
using formula deltaV=V* ɑ deltaT, we have deltaT=deltaV/(V ɑ), and deltaV=hS=h pi d^2/4. deltaT=h pi d^2/(4 V ɑ)=0.05 3.14 0.15 0.15/(4 255* 0.18×10^(−3))=0.01924
Looking at the units of the thermal expansion coefficient we can deduce that this coefficient multiplied by the temperature yields some sort of percentage, or fractional change of the volume.
We can find the minimum volume change needed by calculating the volume of a 0.05 mm thick slice of the thermometer.
V = π × 0 . 0 0 5 c m × 0 . 0 0 7 5 c m 2 = 8 . 8 3 × 1 0 − 7 c m 3 (Units converted to cm to work conveniently with the given mercury container volume)
To find out what fractional change this corresponds to, we divide this change in volume by the given volume
F r a c t i o n a l C h a n g e = V δ V = 0 . 2 5 5 c m 3 8 . 8 3 × 1 0 − 7 c m 3 = 3 . 4 6 5 × 1 0 − 6
Now, we finish by calculating what temperature is required for this fractional change.
F r a c t i o n a l C h a n g e = V o l . C o e f f × δ T
δ T = V o l . C o e f f F r a c t i o n a l C h a n g e = 0 . 1 8 × 1 0 − 3 K 1 3 . 4 6 5 × 1 0 − 6 = 0 . 0 1 9 3 K
However, since a change of 1 degree Kelvin is equal to a change of 1 degree Celsius, we can conclude that a change of 0.0193 degrees Celsius is the minimum change detectable by the naked eye.
The volume of the mercury will expand Δ V = α Δ T V 0 . That volume pushes the mercury inside the tube, and we can read it off as a height distance of h = A Δ V . Since h can minimally be 0 . 0 5 mm , we get that Δ T m i n = α V 0 A h = 0 . 0 1 9 3 ∘ C .
Simply applying expression : Co-efficient of volume expansion ( g a m m a ) = d e l t a V / V ∗ 1 / d e l t a T we can solve for d e l t a T .
Given is,
Our known equation about real expansion of liquid ,
Δ V = γ r V ∘ Δ θ
⟺ Δ θ = γ r V ∘ Δ V
⟺ Δ θ = γ r V ∘ π r 2 h
⟺ Δ θ = . 1 8 − 3 K − 1 × 2 5 5 m m 3 π ( . 0 7 5 m m ) 2 ( . 0 5 m m )
⟺ Δ θ ≈ 0 . 0 1 9 3 K = 0 . 0 1 9 3 ∘ C
And that's the answer!