Admittance of parallel two-component circuit?
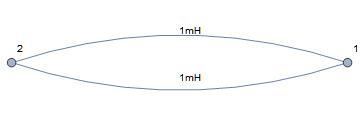
Steven Chase indicated that I have an error in my diagram.
So I do. The lower inductor should have been a 1nF capacitor.
I had specified a 1nF capacitor in that position in my description of the circuit used to draw the diagram. Unfortunately, I forgot that Wolfram Matchematica 11.3.0 has problems drawing diagrams of graphs with multiple edges connecting a pair of nodes. It is my error for not checking for that error in this case.
This is an AC circuit operating at a frequency of . The inductors are 1 mH and the capacitors are 1 nF.
Simplifying assumptions: the components are pure, ideal components, there is no mutual inductance between the inductors and the wiring is negligible.
The device impedance formulae are simple and the frequency was chosen to give integer impedance magnitudes, in the sense that a unit circle in the complex plane has a magnitude of around the entire circle. The standard unit for inductors is a Henry and for capacitors is a Farad. Convert the units used above to those units before computing the device impedances.
Here are the necessary formulas.
Please, note well, the admittance and not the impedance is requested.
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The admittance of the inductor is 1 0 0 0 i 1 or − 1 0 0 0 i . The admittance of the capacitor is − 1 0 0 0 i 1 or 1 0 0 0 i . Adding the admittances, which is correct for parallel circuits, gives 0 as the result.