Geometry of Methane
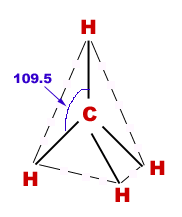 Mathematically, the correct value of angle between any two C-H bonds in Methane molecule is
Mathematically, the correct value of angle between any two C-H bonds in Methane molecule is
where and are coprime positive integers. Find the value of .
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Each C-H bond is a radius of circunsphere of regular tetrahedron with vertexes in each H.
Let A , B , C , D be these 4 vertex. Let face A B C be called "base" of our regular tetrahedron and O be the center of insphere and circumsphere. The base is an equilateral triangle .
The circumradius lenght and inradius lenght are 3 : 1 in a regular tetrahedron. Let the inradius be 1, and we can easy find by Pythagorean Theorem the projetion A O ´ of circumradius A O at base. Then, A O ´ = 8 .
A O ´ is the radius of circumcircle of base, so we can find the base side (edge of tetrahedron). It will be A B = 2 6 .
I would prefer find the asked angle ( ∠ A O B , known as the tetrahedral angle) applying cosine rule in triangle A O B , which gives a prettier result: just c o s − 1 ( − 1 / 3 ) . But the question describe that angle as 2 c o s − 1 ( a / b ) , so we need to consider the right triangle O A M (M is the midpoint of AB).
By Pythagorean Theorem we get O M = 3 , so c o s ( ∠ A O M ) = 3 3 = 9 3 = 1 / 3 .
Finally, the asked angle is 2 c o s − 1 ( 1 / 3 ) and the answer is a + b = 4 .