Advanced geometry problem
Orange shape of a size 5.655 cm^2 is making one fifth of the area of a cricle and |PR| = 1.4 cm. Calculate the area of the blue circle segment using following rules:
1. Every result round up to 3 signifficant digits
2. Use Pi button on a calculator or (3.141592654)
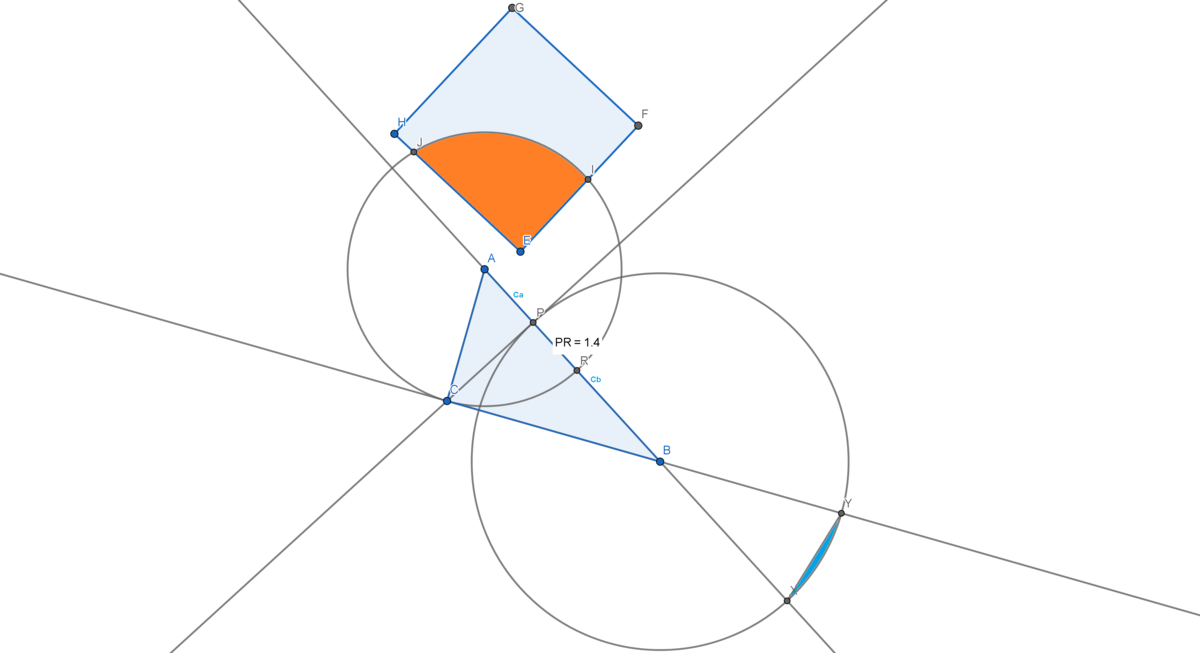
The answer is 0.236.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since we know that orange shape is making one fifth of the area of a cricle, we can calculate its radius: S E O P = 5 1 × S C S C = 5 × 5 . 6 5 5 = 2 8 . 2 7 4 c m 2 = 3 c m 2 S C = π × r 1 2 ⇒ r 1 = π S C = π 2 8 . 2 7 4 \buildrel . We can notice that: r 1 = b c a = r 1 − ∣ P R ∣ = 3 − 1 . 4 = 1 . 6 c m By using Pythagorean theorem, we can calculate a height from the point C : v c = b 2 − c a 2 = 3 2 − 1 . 6 2 = 2 . 5 3 8 c m By using Euclid's formula, we can calculate 2nd part of the side c : v c 2 = c a × c b ⇒ c b = c a v c 2 = 1 . 6 2 . 5 3 8 2 = 4 . 0 2 6 c m Via trigonometric formula for sin , we can calculate angle beta : sin ( β ) = c b ⇒ β = arcsin ( c b ) = arcsin ( 4 . 0 2 6 + 1 . 6 3 ) = 3 2 . 2 We can tell, that: β = δ Where delta is XBY angle and also for the radius of a 2nd circle: r 2 = c b Our last step involves a formula for a circle segment: S = 2 1 × r 2 2 ( 1 8 0 π × δ − sin ( δ ) ) = 2 1 × 4 . 0 2 6 2 ( 1 8 0 π × 3 2 . 2 − sin ( 3 2 . 2 ) ) = 0 . 2 3 6 c m 2