Advanced spring mechanics
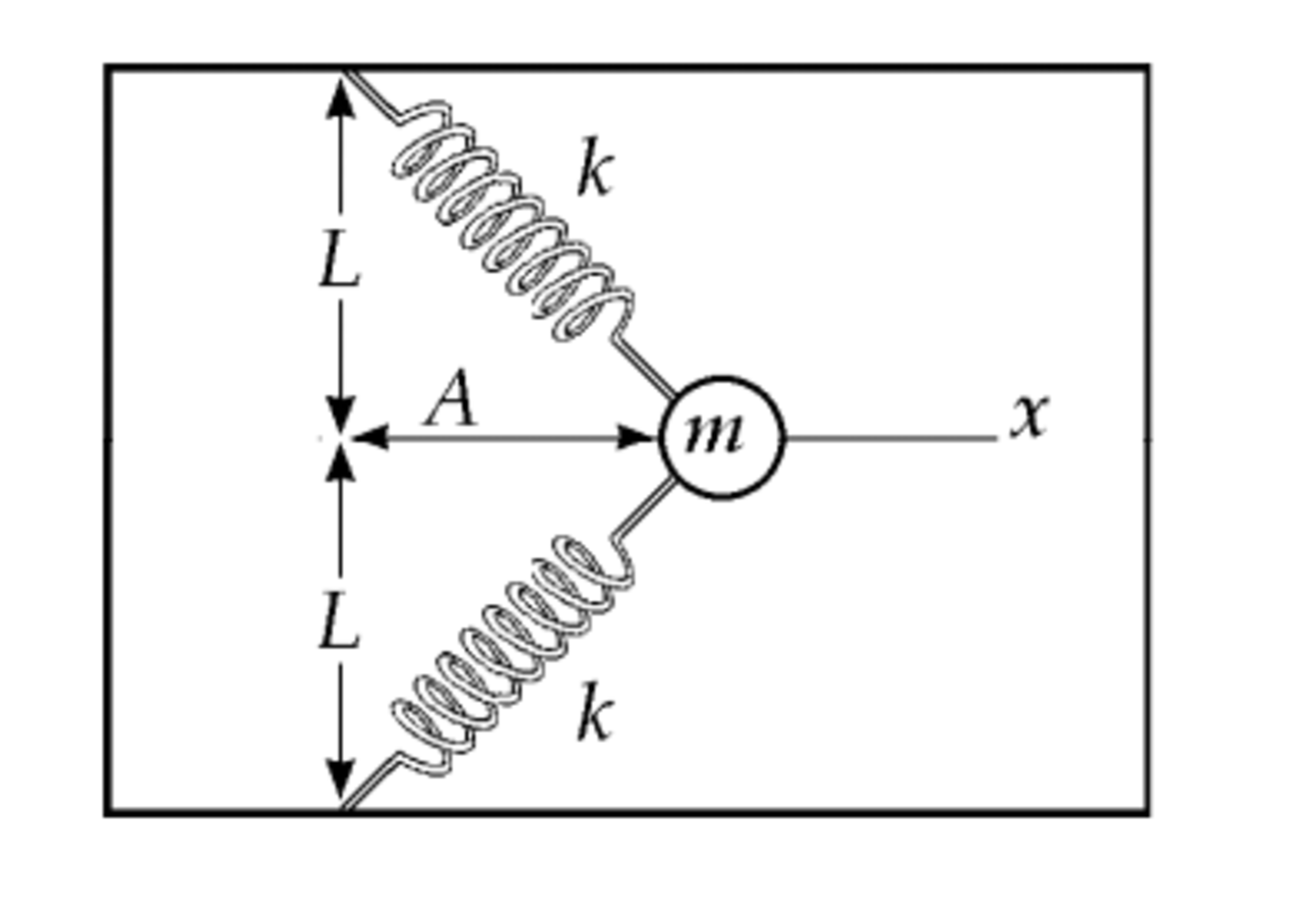
The following diagram shows a block of mass m = 1 k g attached to two identical springs of natural length L = 1 meters and spring constants k = 1 N/m. The block is pulled along the + x -axis by a length of x = 3 meters; when it is released, the block moves with an acceleration x ¨ in the − x direction. Find the initial acceleration of the block and the time it takes to reach the origin x = 0 .
Enter your answer as t + a , where t is the time it takes for the block to reach the origin and a is the magnitude of the initial acceleration of the block.
The answer is 5.51641540387.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I agree with @Steven Chase . A nice problem indeed. Also posting my solution, which is a semi-analytical approach.
Consider the block at a general time instant t . Its kinetic energy is:
T = 2 1 m x ˙ 2
The system is symmetrical about the X-axis and the springs are identical. The potential energy of each spring is the same and the total potential energy of the system is therefore:
V = 2 ( 2 1 K ( x 2 + 1 − 1 ) 2 ) V = K ( x 2 + 1 − 1 ) 2
The total energy of the system is a constant which is equal to the initial potential energy of the system. Note that initially the particle is at x = 3 and is released from rest. This gives:
T + V = K ( 1 0 − 1 ) 2 ⟹ 2 1 m x ˙ 2 + K ( x 2 + 1 − 1 ) 2 = K ( 1 0 − 1 ) 2 ⟹ 2 1 x ˙ 2 + ( x 2 + 1 − 1 ) 2 = ( 1 0 − 1 ) 2 Re-arranging gives:
⟹ x ˙ = − 2 ( ( 1 0 − 1 ) 2 − ( x 2 + 1 − 1 ) 2 )
The additional negative sign is included to imply that as time progresses, x decreases.
Separating the variables and integrating gives the required time period:
∫ 0 3 2 ( ( 1 0 − 1 ) 2 − ( x 2 + 1 − 1 ) 2 ) d x = T ≈ 1 . 4 1 3 8
To find the initial acceleration, consider the energy conservation equation:
⟹ 2 1 x ˙ 2 + ( x 2 + 1 − 1 ) 2 = ( 1 0 − 1 ) 2
Differentiating the above with respect to time gives:
( x ¨ + 2 x ( 1 − x 2 + 1 1 ) ) x ˙ = 0
Since x ˙ cannot be zero, the term:
x ¨ + 2 x ( 1 − x 2 + 1 1 ) = 0
At the initial instant when the block is just released, the magnitude of the acceleration of the block is obtained by substituting x = 3 above, which gives:
∣ x ¨ ( 0 ) ∣ ≈ 4 . 1 0 2 6 3 3
The required answer is, therefore:
∣ x ¨ ( 0 ) ∣ + T ≈ 5 . 5 1 6 4
Very nice solution.
brilliant way to find the final time.
Log in to reply
Thank you. This approach applies to systems where energy is conserved.
Nice problem. Simulation code attached below (with comments)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 |
|
Thanks for solving!
I will going to use the Newtonian model for finding out the forces acting on the block, so let's first draw a free body diagram for one of the springs:
Let's call the force the spring applies on the block directly F s . The vertical and horizontal components respectively are:
F y = F s sin ( θ ) and F x = F s cos ( θ )
The vertical component of the forces exerted by both springs are opposite in direction and cancel each other out.
Where cos ( θ ) = L 2 + x 2 L
A single spring's stretch is equal to L 2 + x 2 − L , so the force a single spring exerts on the block is k ( L 2 + x 2 − L )
So the force both springs exert on the object is m x ¨ = − 2 k x ( 1 − L 2 + x 2 1 )
Since the block is of unit mass, the initial acceleration is also − 2 k x ( 1 − L 2 + x 2 1 ) = 4 . 1 0 2 6 6 m/ s 2
@Karan Chatrath analytically found out the integral which gives the time it takes for the block to reach the origin by integrating x ˙ 1 over distance. He did it by using energy conservation.
Here is my numerical simulation which uses Explicit Euler numerical integration: