Adventitious Quadrangle 4
Find x in degrees.
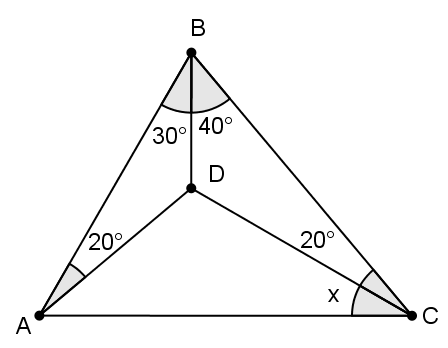
Bonus: Solve without trigonometry.
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Your solution is good. I tried a simple way way And that is by straightning the BD line to the bottom until we get 90 degree angel. We add it up with the BDC angel, equals 150 -180= 30
Log in to reply
we dont know if BD and AC are perpendicular (90 deg), unless proven.
What I like about this problem is how there are many different ways to solve it. First, find m ∠ D , m ∠ E , and m ∠ F :
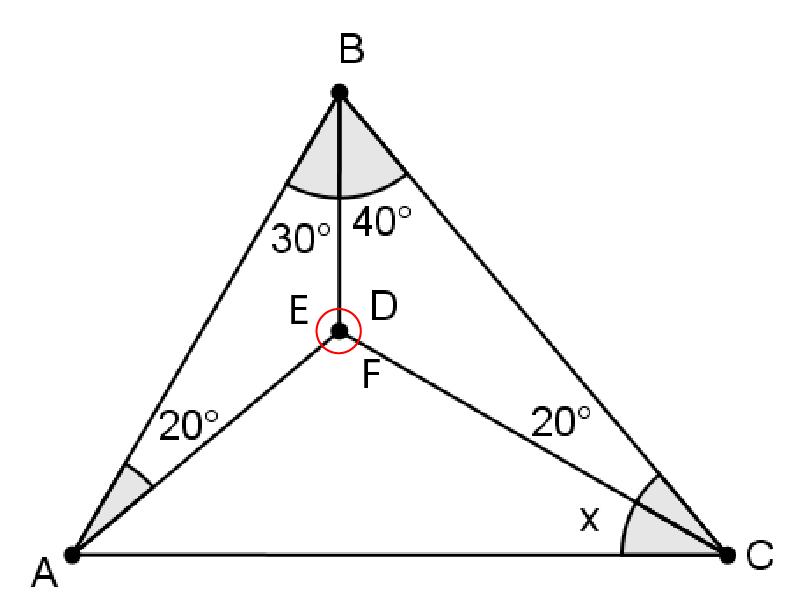
D = 1 8 0 − ( 4 0 + 2 0 ) = 1 2 0 ∘ E = 1 8 0 − ( 3 0 + 2 0 ) = 1 3 0 ∘ F = 3 6 0 − ( D + E ) = 3 6 0 − ( 1 2 0 + 1 3 0 ) = 1 1 0 ∘
Since we have labeled F , we now have a formula for x : x + F + ( A − 2 0 ) = 1 8 0 Then, draw a perpendicular bisector from B to A C :
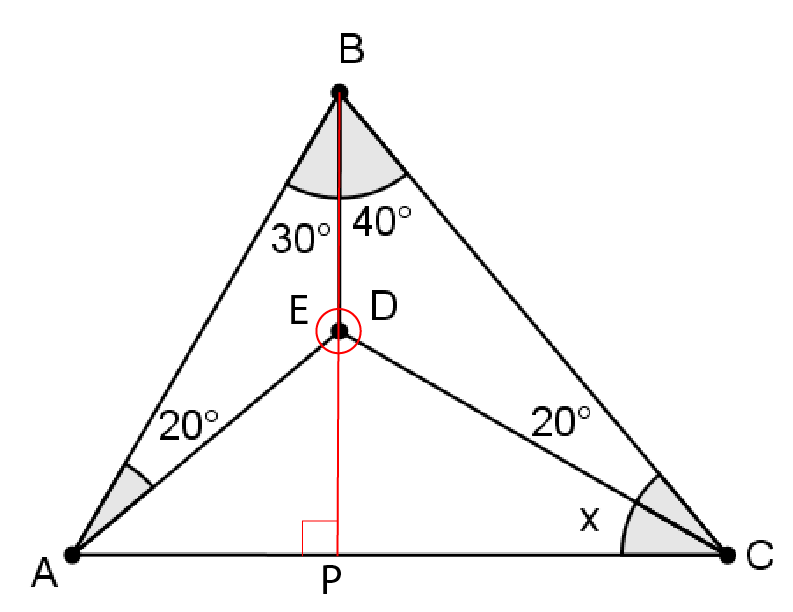
Note that since m ∠ A B D = 3 0 ∘ , △ A B P is a 30-60-90 triangle. Therefore, m ∠ A = 6 0 ∘ .
Finally,
x + F + ( A − 2 0 ) = 1 8 0 x = 1 8 0 − 1 1 0 − 4 0 = 3 0 ∘
unfortunately, the reasoning is incorrect, we cant know if extending BD to P result in right angle triangle, you have to prove it. either:
-
extend BD to meet AC at P and prove APB is 90 degree, or
-
construct P on AC such that BPA is 90 degree and prove that BDP are collinear.
in other words, we cant simultaneously ask for BDP collinear and BPA 90 degree, we have too few freedom of choice.
Log in to reply
I think you've stumped us, then. Could you please elaborate how to solve in your solution?
Log in to reply
the first 2 steps are similar to yours. when i reflect D to D', that forms a kite, whose diagonals are perpendicular. this is equivalent to construct line AD' perpendicular to BC. next i prove that ADD' is collinear by simple angle chasing.
notice that i did not "ask" for 90degree and collinear at the same time, i construct one and prove the other.
the rest make use of cyclic quadrilateral (which isnt quite relevant to this discussion).
another way to understand why your solution isnt valid, is that changing some angle make it obviously doesnt work.
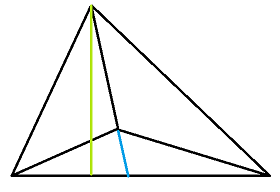 notice that the blue line extends AD while the green line construct perpendicular line, the 2 doesnt coincides. hopefully that helps.
notice that the blue line extends AD while the green line construct perpendicular line, the 2 doesnt coincides. hopefully that helps.
From trigonometric version of Ceva's theorem, we know that:
s i n ∠ C B D s i n ∠ D B A ⋅ s i n ∠ D A B s i n ∠ C A D ⋅ s i n ∠ A C D s i n ∠ D C B = 1
⇒ s i n 4 0 s i n 3 0 ⋅ s i n 2 0 s i n ( 7 0 − x ) ⋅ s i n x s i n 2 0 = 1
Now it's only calculations:
s i n 4 0 s i n 3 0 ⋅ s i n x s i n 7 0 c o s x − c o s 7 0 s i n x = 1
t a n x s i n 7 0 − c o s 7 0 t a n x = s i n 3 0 s i n 4 0
t a n x = s i n 3 0 s i n 4 0 + c o s 7 0 s i n 7 0 ⇒ x = 3 0
Angle BDC=120°, Angle ADB=130° so Angle ADC=110°. Point D is the ortho-centre of ∆ABC as Angle ADC=180°-70= 110°. So angle BDA=180°-Angle C. Substituting we get Angle ACB as 50°. So x=30°
if D is orthocenter then ∠ A D C = 1 8 0 − ∠ A B C , but the converse is not true.
to see why, construct a circle passing through A D C . any point P on the arc A D C satisfy ∠ A P C = ∠ A D C
hint:
reflect D about B C .
show that A D D ′ is a straight line.
show that A B D ′ C is a cyclic quadrilateral by inscribed angle theorem.
show that x = 3 0 ∘ .