Adventitious Quadrangle 6
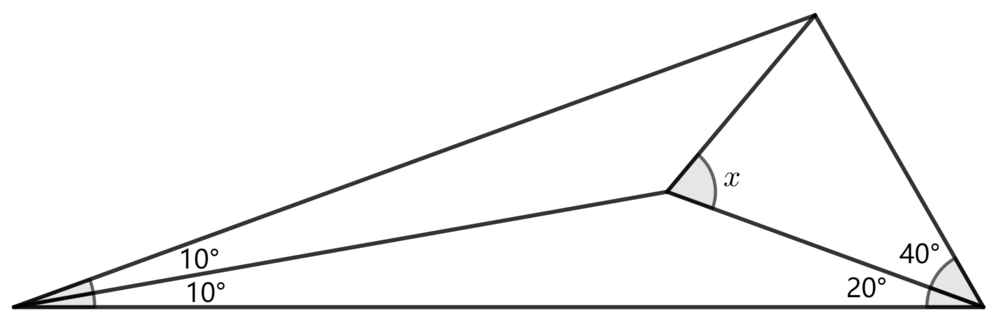
What is the measure of angle x in degrees?
Bonus: Solve it without trigonometry.
The answer is 70.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
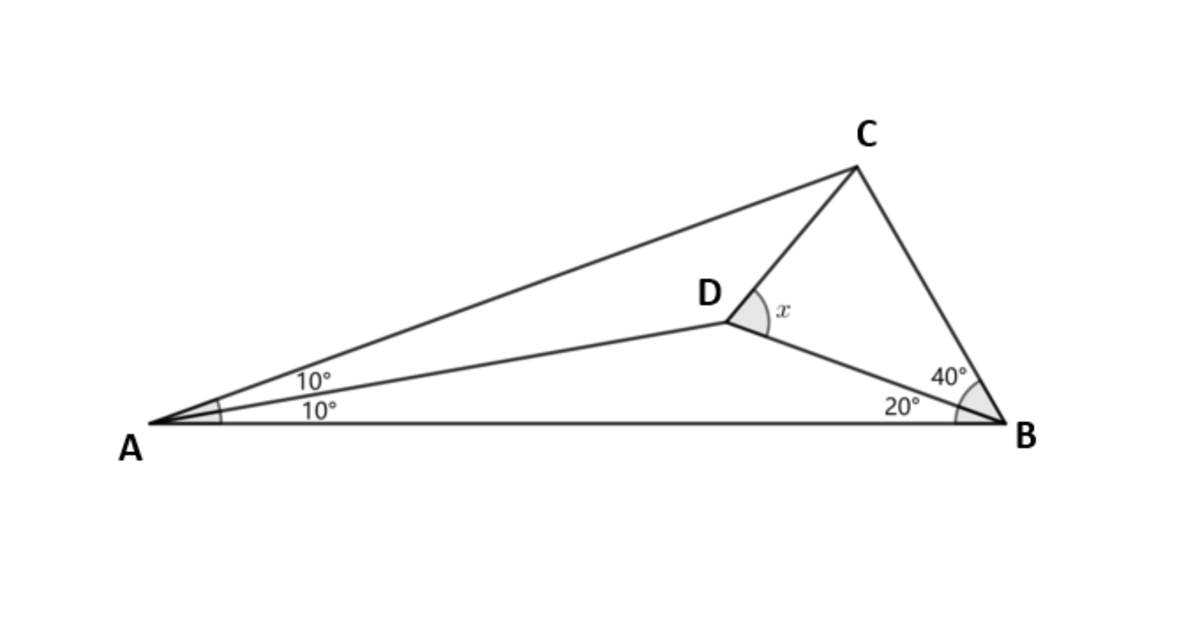
For the triangle above, we have:
∠ B C D = ( 1 4 0 − x ) ∘ and ∠ D A B = ( x − 4 0 ) ∘
In addition, we have
D A D C D B D A D C D B = 1
Now, applying the law of Sines, to triangles △ D C A , △ D A B , and △ D B C , in this order, the above equation becomes,
sin ( x − 4 0 ) ∘ sin 1 0 ∘ sin 1 0 ∘ sin 2 0 ∘ sin 4 0 ∘ sin ( 1 4 0 − x ) ∘ = 1
which reduces to,
sin 2 0 ∘ sin ( 1 4 0 − x ) ∘ = sin ( x − 4 0 ) ∘ sin 4 0 ∘
Using the identity sin ( A ± B ) = sin A cos B ± cos A sin B , results in
sin 2 0 ∘ ( sin 1 4 0 ∘ cos x ∘ − cos 1 4 0 ∘ sin x ∘ ) = sin 4 0 ∘ ( sin x ∘ cos 4 0 ∘ − cos x ∘ sin 4 0 ∘ )
Dividing through by cos x ∘ and re-arranging, we obtain,
tan x ∘ = sin 4 0 ∘ cos 4 0 ∘ + sin 2 0 ∘ cos 1 4 0 ∘ sin 2 0 ∘ sin 1 4 0 ∘ + sin 2 4 0 ∘
Using a scientific calculator, we can now find tan x ∘ , and then using the tan − 1 function we can find x ∘ . The answer comes to 7 0 ∘
Label the figure as above, where D E = h 1 and A F = h 2 are perpendicular to B C = 1 , and D G is parallel to B C . Then we have:
h 1 cot 1 0 ∘ + h 1 cot 2 0 ∘ = 1
⟹ h 1 = tan 1 0 ∘ + tan 2 0 ∘ tan 1 0 ∘ tan 2 0 ∘ = sin 1 0 ∘ cos 2 0 ∘ + sin 2 0 ∘ cos 1 0 ∘ sin 1 0 ∘ sin 2 0 ∘ = sin 3 0 ∘ sin 1 0 ∘ sin 2 0 ∘ = 2 sin 1 0 ∘ sin 2 0 ∘
Similarly, h 2 cot 2 0 ∘ + h 2 cot 6 0 ∘ = 1 , ⟹ h 2 = sin 8 0 ∘ sin 2 0 ∘ sin 6 0 ∘ = cos 1 0 ∘ 2 sin 1 0 ∘ cos 1 0 ∘ sin 6 0 ∘ = 3 sin 1 0 ∘
Then we note:
tan ∠ A D G tan ( x − 2 0 ∘ ) ⟹ x = D G A G = h 1 cot 2 0 ∘ − h 2 cot 6 0 ∘ h 2 − h 1 = 2 sin 1 0 ∘ cos 2 0 ∘ − sin 1 0 ∘ 3 sin 1 0 ∘ − 2 sin 1 0 ∘ sin 2 0 ∘ = 2 cos 2 0 ∘ − 1 3 − 2 sin 2 0 ∘ = cos 2 0 ∘ − 2 1 2 3 − sin 2 0 ∘ = cos 2 0 ∘ − cos 6 0 ∘ cos 3 0 ∘ − cos 7 0 ∘ = 2 sin 2 0 ∘ sin 4 0 ∘ 2 sin 2 0 ∘ sin 5 0 ∘ = cos 5 0 ∘ sin 5 0 ∘ = tan 5 0 ∘ = 7 0 ∘ Divide up and down by 2