Aesthetically pleasing, somehow
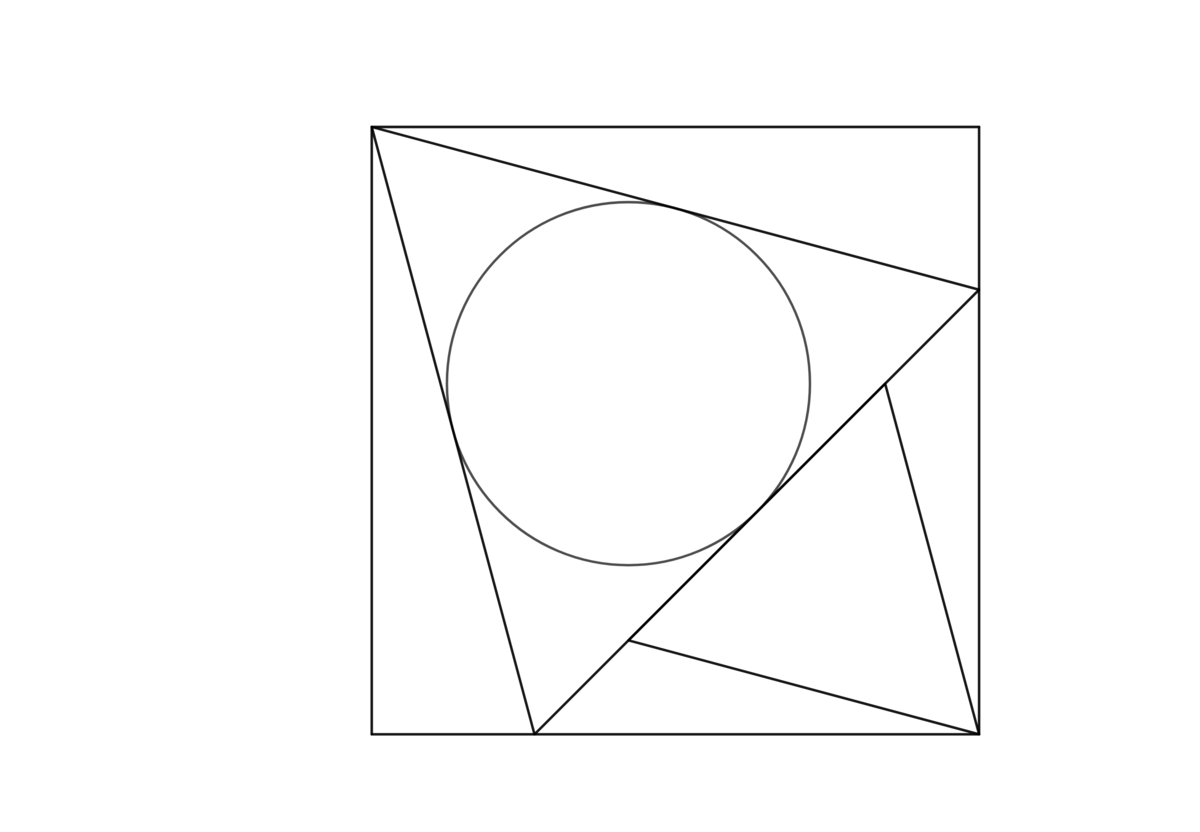
The figure shows two equilateral triangles symmetrically positioned along the diagonal of a unit square. What is the inradius of the larger triangle? Express it as , where and are square-free integers. Submit .
Extra credit: show that it is one half the side of the smaller triangle.
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the side of the larger equilateral triangle be s and the side of the smaller equilateral triangle be t , and label the diagram as follows:
Since the angle of the square is 9 0 ° and the angle of the equilateral triangle is 6 0 ° , by symmetry ∠ B A C = 2 1 ( 9 0 ° − 6 0 ° ) = 1 5 ° , so s = cos 1 5 ° 1 = 6 − 2 .
The inradius of the larger equilateral triangle is r s = 2 3 1 s = 2 3 1 ( 6 − 2 ) = 2 2 − 6 6 .
Therefore, a = 2 , b = 6 , and a + b = 8 .
Extra credit:
The height of the larger equilateral triangle is h s = 2 3 s and the height of the smaller equilateral triangle is h t = 2 3 t . Since the triangles are placed along the diagonal of the unit square, h s + h t = 2 , or 2 3 s + 2 3 t = 2 , which rearranges to 2 t = 3 6 − 2 1 s .
Substituting s = 6 − 2 , we find that 2 t = 3 6 − 2 1 ( 6 − 2 ) = 2 2 − 6 6 = r s .