Affixing squares
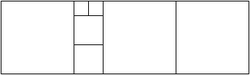 Starting with a square of the size
, you may do the following operation any number of times (including none at all): choose one side of the rectangle you have and affix a square to that side, with length equal to that side. The image above shows one possibility.
Starting with a square of the size
, you may do the following operation any number of times (including none at all): choose one side of the rectangle you have and affix a square to that side, with length equal to that side. The image above shows one possibility.
Determine the number of ordered pairs of integers , with , such that you can obtain a rectangle of size .
The answer is 6087.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
All pairs ( l , w ) with g cd ( l , w ) = 1 are possible, and only those. A simple algorithm can print the result 6 0 8 7 , such as this:
It remains to show that the above claim is correct.
Observe that it doesn't matter whether you put a square on the left side or on the right side; likewise, it doesn't matter whether you put a square on the top side or on the bottom side. So we can just say whether we extend the rectangle horizontally or vertically.
Moreover, given a rectangle l × w ( l units horizontally, w units vertically), we can always determine the last move. If l > w , then the last move must have been affixing w × w horizontally on a ( l − w ) × w rectangle; the other possibility is impossible as there's no rectangle left. If l < w , the last move was vertical. If l = w , then there's no last move.
Now observe that this is exactly the Euclidean algorithm! Whichever number is smaller, subtract it from the larger one. Repeat until both numbers are equal, which gives the GCD.
Thus, if l × w can be generated from 1 × 1 , it must be that g cd ( l , w ) = 1 . Likewise, every pair with GCD 1 can be generated by just reversing the sequence of steps generated by the Euclidean algorithm. For example, for the picture,
g cd ( 1 7 , 5 ) = g cd ( 1 2 , 5 ) = g cd ( 7 , 5 ) = g cd ( 2 , 5 ) = g cd ( 2 , 3 ) = g cd ( 2 , 1 ) = g cd ( 1 , 1 )
Reversing the sequence above, from 1 × 1 we extend horizontally to 2 × 1 , then vertically twice to 2 × 5 , then horizontally three times to 1 7 × 5 . This shows the correctness of the claim.