This can't be that Short!
k = 1 ∑ m [ ( k 2 + 1 ) k ! ] = 1 9 9 9 × 2 0 0 0 !
What value of m satisfies the above summation?
The answer is 1999.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Nicely done ! :)
We know r ∗ r ! = [ ( r + 1 ) − r ] r ! = ( r + 1 ) ! − r ! .
So, ( k 2 + 1 ) k ! = k ( k ∗ k ! ) + k !
= k [ ( k + 1 ) ! − k ! ] + k !
= [ ( k + 2 ) − 2 ] ( k + 1 ) ! − k ∗ k ! + k !
= ( k + 2 ) ! − 2 ( k + 1 ) ! − ( k + 1 ) ! + 2 k !
= [ ( k + 2 ) ! − ( k + 1 ) ! ] − 2 [ ( k + 1 ) ! − k ! ]
Now, ∑ k = 1 m [ ( k 2 + 1 ) k ! ]
= ∑ k = 1 m [ ( k + 2 ) ! − ( k + 1 ) ! ] − 2 ∑ k = 1 m [ ( k + 1 ) ! − k ! ]
= ( m + 2 ) ! − 2 ! − 2 [ ( m + 1 ) ! − 1 ] = ( m + 1 ) ! [ m + 2 − 1 ] = m ∗ ( m + 1 ) ! = 1 9 9 9 ∗ ( 2 0 0 0 ) !
So, m = 1 9 9 9 .
On the first line:r r!=[(r+1)-1] r!
( k 2 + 1 ) k ! = { ( k + 2 ) ( k + 1 ) − 3 ( k + 1 ) + 2 } k ! = ( k + 2 ) ! − 3 ( k + 1 ) ! + 2 k ! = { ( k + 2 ) ! − ( k + 1 ) ! } − 2 { ( k + 1 ) ! − k ! } t e l e s c o p i n g . . . k = 1 ∑ m ( k 2 + 1 ) k ! = { ( m + 2 ) ! − 2 ! } − 2 { ( m + 1 ) ! − 1 ! } = { ( m + 2 ) ! − 2 ( m + 1 ) ! } − { 2 ! − 2 . 1 ! } = m ( m + 1 ) ! = 1 9 9 9 × 2 0 0 0 ! ⇒ m = 1 9 9 9
nice solution thnxx
Note: The following solution is hinted by an online friend FAlin from Taiwan's forum telnet://ptt.cc or https://www.ptt.cc/bbs/Math/
Note that ( k 2 + 1 ) k ! = ( k 2 + k − k + 1 ) k ! = [ k ( k + 1 ) − ( k − 1 ) ] k ! = k ( k + 1 ) ! − ( k − 1 ) k ! then
∑ k = 1 m [ ( k 2 + 1 ) k ! ] = ∑ k = 1 m [ k ( k + 1 ) ! − ( k − 1 ) k ! ] = ∑ k = 1 m [ − ( k − 1 ) k ! + k ( k + 1 ) ! ]
= [ − 0 ∗ 1 ! + 1 ∗ 2 ! ] + [ − 1 ∗ 2 ! + 2 ∗ 3 ! ] + [ − 2 ∗ 3 ! + 3 ∗ 4 ! ] + [ − 3 ∗ 4 ! + 4 ∗ 5 ! ] + [ − 4 ∗ 5 ! + 5 ∗ 6 ! ] + . . . (telescoping)
+ [ − ( m − 1 ) m ! + m ( m + 1 ) ! ] = m ( m + 1 ) !
Therefore, 1999*2000! = ∑ k = 1 1 9 9 9 [ ( k 2 + 1 ) k ! ] , m=1999
follow up question: is your observation correct?
sounds interesting, though a simple mathematical induction would suffice..
( k 2 + 1 ) ( k ! ) is: For k 1 = ( 1 + 1 ) ( 1 ! ) = 2
For k 2 = ( 4 + 1 ) ( 2 ! ) = 1 0
For k 3 = ( 9 + 1 ) ( 3 ! ) = 6 0
For k 4 = ( 1 6 + 1 ) ( 4 ! ) = 4 0 8
For k 5 = ( 2 5 + 1 ) ( 5 ! ) = 3 1 2 0
Let S k i = k = 1 ∑ k i [ ( k 2 + 1 ) ( k ! ) ]
S k 1 = 2 ⇒ 2 ! × 1
S k 2 = 1 2 ⇒ 3 ! × 2
S k 3 = 7 2 ⇒ 4 ! × 3
S k 4 = 4 8 0 ⇒ 5 ! × 4
By induction proof that: k = 1 ∑ m = ( m ) ( m + 1 ) !
Step 1 k = 1 ∑ 1 [ ( k 2 + 1 ) ( k ! ) ] = ( 1 ) ( 1 + 1 ) ! = 2 k 1 = ( 1 + 1 ) ( 1 ! ) = 2
Step 2 k = 1 ∑ m = ( m ) ( m + 1 ) ! is true.
Step 3 Proof that k = 1 ∑ m + 1 = ( m + 1 ) ( m + 2 ) ! k = 1 ∑ m + 1 [ ( k 2 + 1 ) ( k ! ) ] = ( m ) ( m + 1 ) ! + ( ( m + 1 ) 2 + 1 ) ( m + 1 ) ! k = 1 ∑ m + 1 [ ( k 2 + 1 ) ( k ! ) ] = ( m ) ( m + 1 ) ! + ( ( m 2 + 2 m + 1 + 1 ) ( m + 1 ) ! k = 1 ∑ m + 1 [ ( k 2 + 1 ) ( k ! ) ] = ( m + 1 ) ! ( m 2 + 3 m + 2 ) k = 1 ∑ m + 1 [ ( k 2 + 1 ) ( k ! ) ] = ( m + 1 ) ! ( m + 2 ) ( m + 1 ) k = 1 ∑ m + 1 [ ( k 2 + 1 ) ( k ! ) ] = ( m + 2 ) ! ( m + 1 ) ■
For S k i = k = 1 ∑ m [ ( k 2 + 1 ) ( k ! ) = 1 9 9 9 × 2 0 0 0 ! m = 1 9 9 9
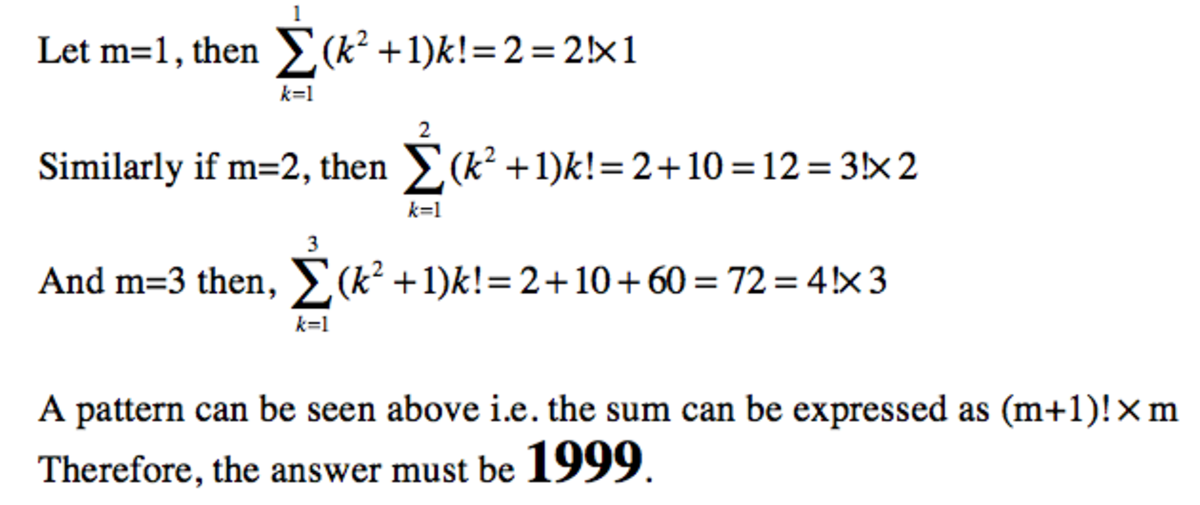
First we prove ∑ i = a b i ∗ i ! = ( b + 1 ) ! − a !
Proof:- ∑ i = a b i ∗ i !
= ∑ i = a b ( i + 1 ) ∗ i ! − i !
= ∑ i = a b ( i + 1 ) ! − i !
= ( a + 1 ) ! − a ! + ( a + 2 ) ! − ( a + 1 ) ! + ⋯ + ( b + 1 ) ! − b !
= ( b + 1 ) ! − a ! .
Now to the question.
∑ k = 1 m ( k 2 + 1 ) k !
= ∑ k = 1 m ( k 2 + 2 k + 1 ) k ! − 2 k ∗ k !
= ∑ k = 1 m ( k + 1 ) 2 k ! − 2 ∑ k = 1 m k ∗ k !
= ∑ k = 1 m ( k + 1 ) ∗ ( k + 1 ) ! − 2 ( ( m + 1 ) ! − 1 ! )
Putting l = k + 1 , l = 2 when k = 1 and l = m + 1 when k = m .
= ∑ l = 0 m + 1 l ∗ l ! − 2 ( m + 1 ) ! + 2
= ( m + 2 ) ! − 2 ! − 2 ( m + 1 ) ! + 2
= ( m + 1 ) ! ( m + 2 − 2 )
= m ∗ ( m + 1 ) !
Comparing with 1 9 9 9 ∗ ( 2 0 0 0 ) ! , we see that m = 1 9 9 9